Лабораторные работы по Основам теории систем
Лабораторная работа № 2
Телешовой Елизаветы, гр. 726,
Цель работы: Решение задач линейного программирования симплекс-методом. Варианты разрешимости задач линейного программирования.
1 вариант.
1. Четыре студента: Иванов, Петров, Сидоров и Васильев пошли на концерт группы «Чайф», захватив пиво 2 сортов: «Русич» и «Премьер». Определить план распития напитков для получения максимального суммарного опьянения (в ![]() ). Исходные данные даны в таблице:
). Исходные данные даны в таблице:
Студент Норма выпитого Запасы
(в литрах)
«Русич» «Премьер» Иванов 2 2 1.5 Петров 3,5 1 1,5 Сидоров 10 4 4,5 Васильев – 1 0,7 Крепость напитка 16 % 10 %
2. Математическая модель.
2.1 Управляемые параметры
x1(л) – количество выпитого пива «Русич».
x2(л) – количество выпитого пива «Премьер».
![]() – решение.
– решение.
2.2 Ограничения
![]() – количество пива «Русич», выпитого Ивановым.
– количество пива «Русич», выпитого Ивановым.
![]() – количество пива «Премьер», выпитого Ивановым.
– количество пива «Премьер», выпитого Ивановым.
![]() – общее количество пива, выпитого Ивановым.
– общее количество пива, выпитого Ивановым.
Общее количество пива, выпитого Ивановым, не превосходит имеющихся у него запасов пива, поэтому:
![]() (л).
(л).
Аналогично строим другие ограничения:
![]() (л).
(л).
![]() (л).
(л).
![]() (л).
(л).
3. Постановка задачи.
Найти ![]() *, где достигается максимальное значение функции цели:
*, где достигается максимальное значение функции цели:
![]()
4. Решение.
![]() при:
при:
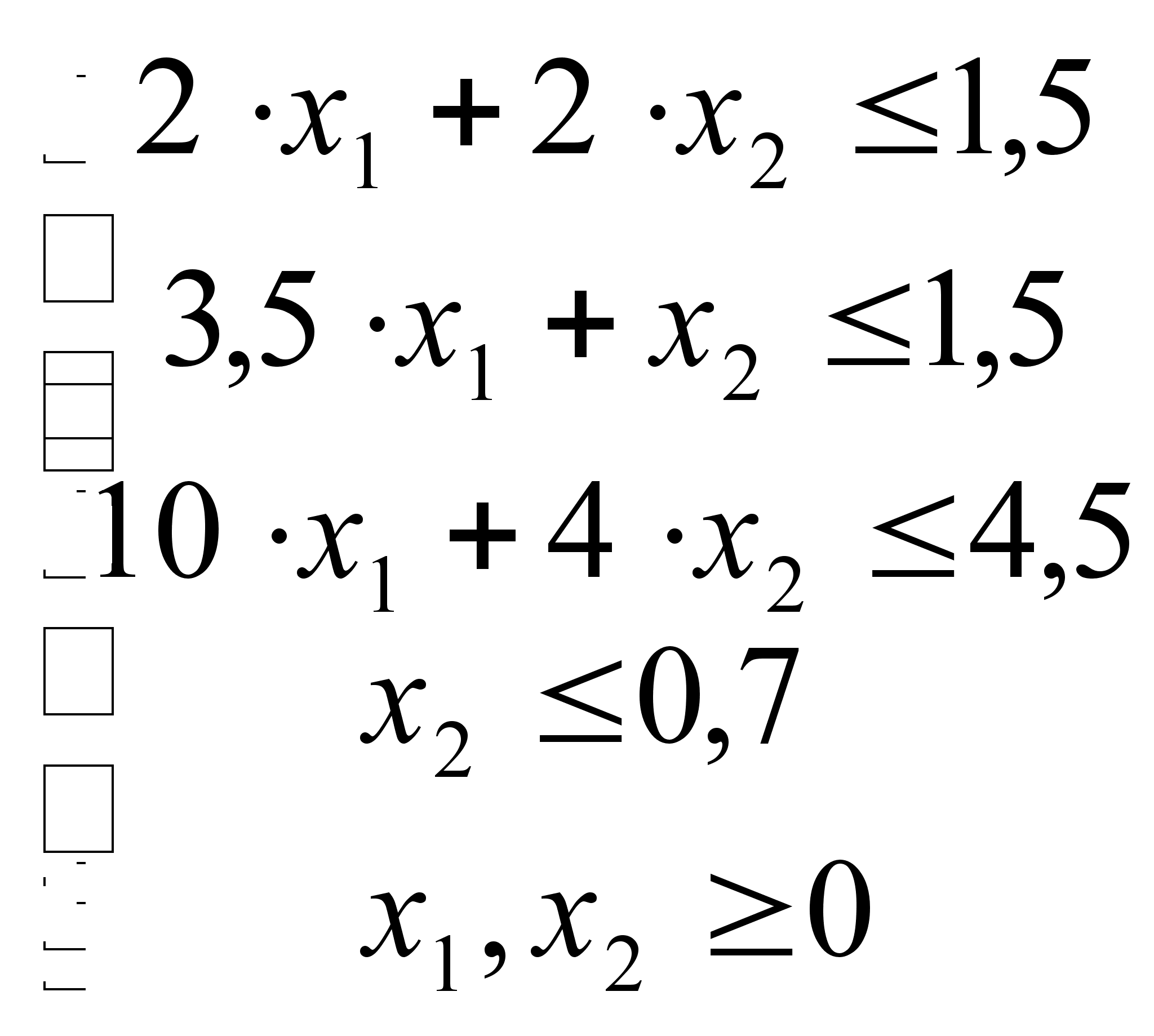
![]()
Приведем задачу к каноническому виду:
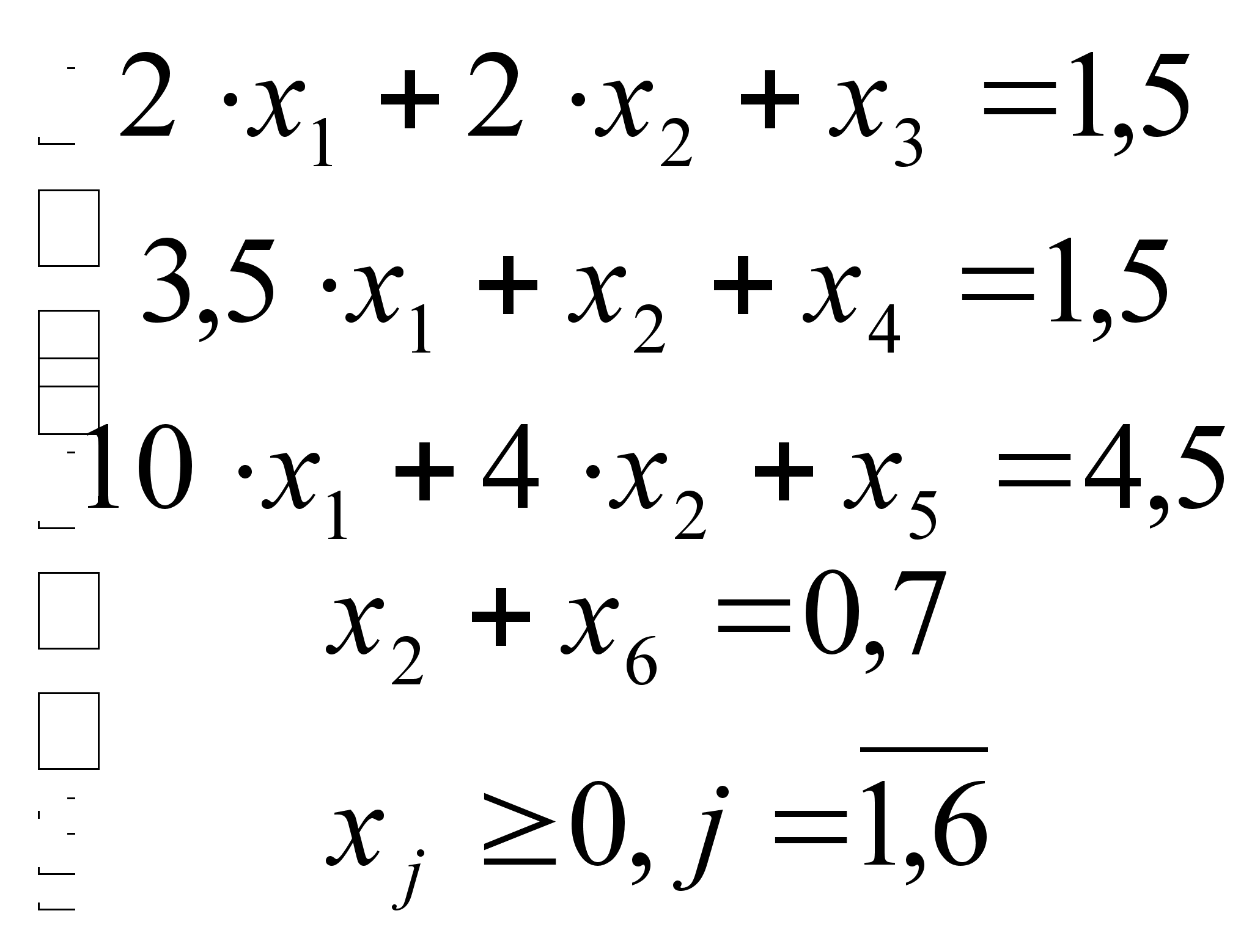
![]()
Определим начальный опорный план: ![]() .
.
Это решение является опорным, т.к. вектора условий при положительных компонентах решения линейно независимы, также ![]() , где
, где ![]() , но не все оценки положительны (
, но не все оценки положительны (![]() , где
, где ![]()
![]() )
)
Опорный план является оптимальным, если для задачи максимизации все его оценки неотрицательны. ![]() не является оптимальным, значит критерий можно улучшить, если увеличить одну их отрицательных свободных переменных. Будем увеличивать
не является оптимальным, значит критерий можно улучшить, если увеличить одну их отрицательных свободных переменных. Будем увеличивать ![]() , т.к. ее увеличение вызовет большее увеличение функции цели.
, т.к. ее увеличение вызовет большее увеличение функции цели.
Предположим, что ![]() , тогда:
, тогда:
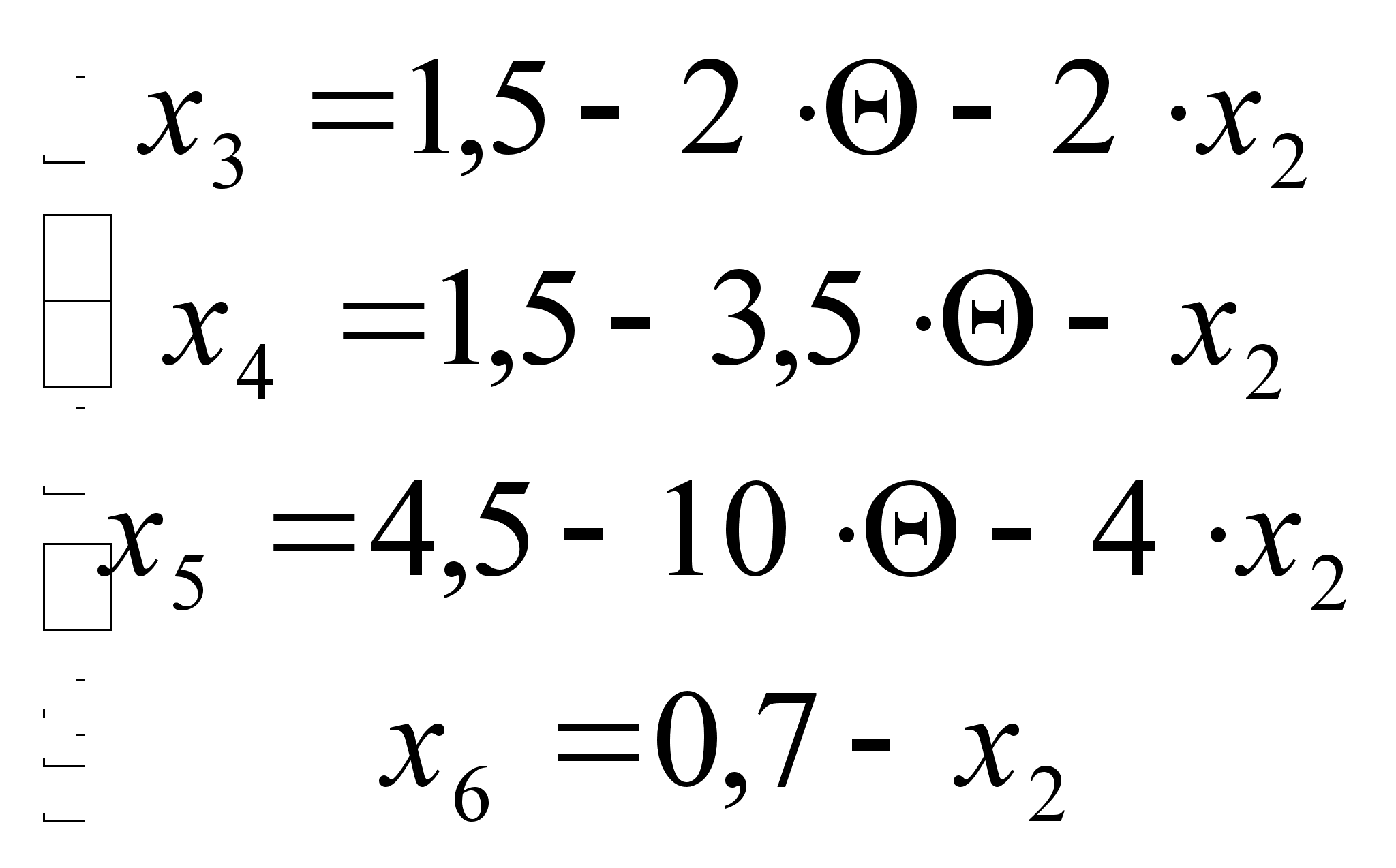
Запишем новый опорный план: ![]() . Все оценки опорного плана должны быть неотрицательны, а значит должны выполняться условия:
. Все оценки опорного плана должны быть неотрицательны, а значит должны выполняться условия:
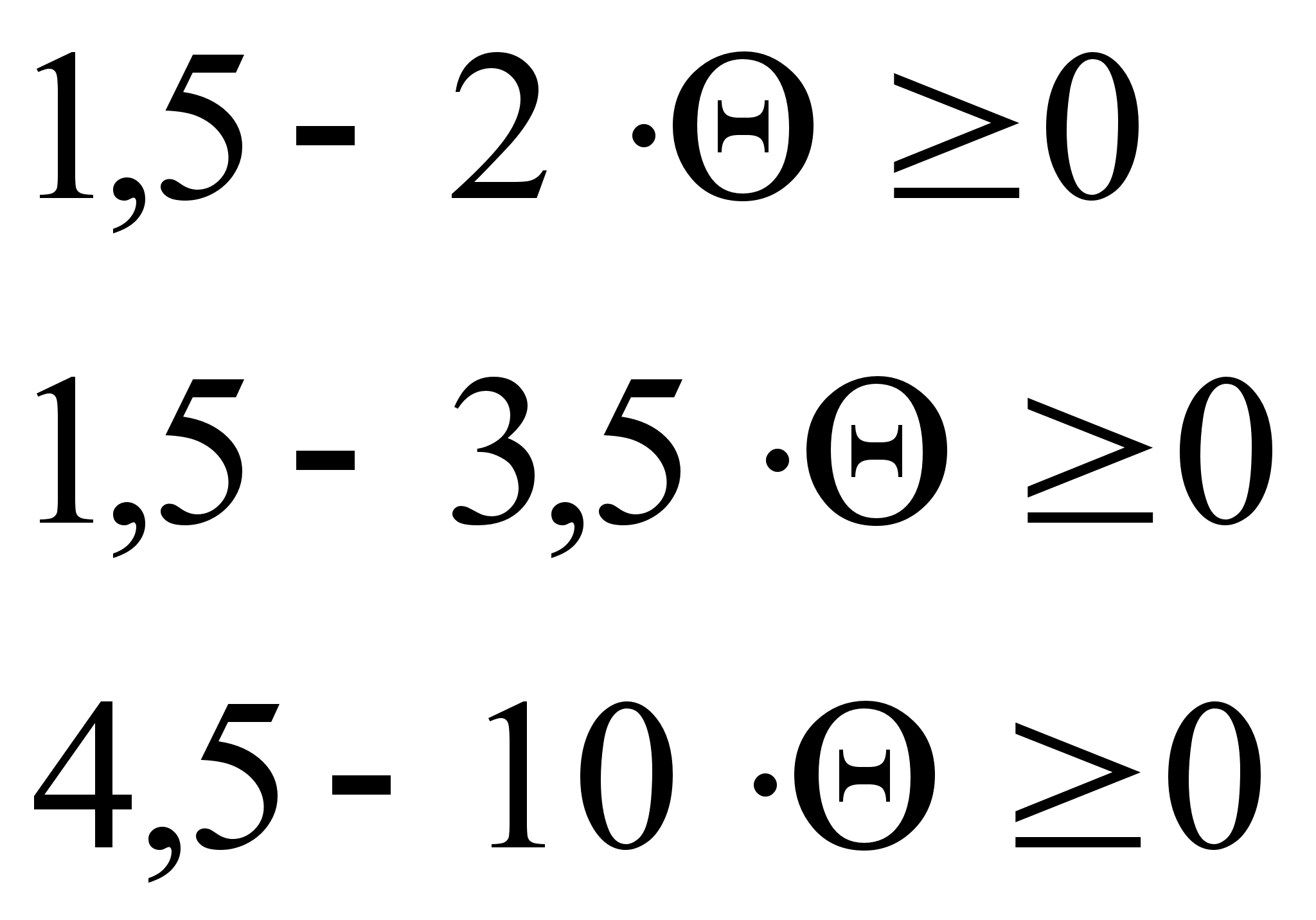 =>
=>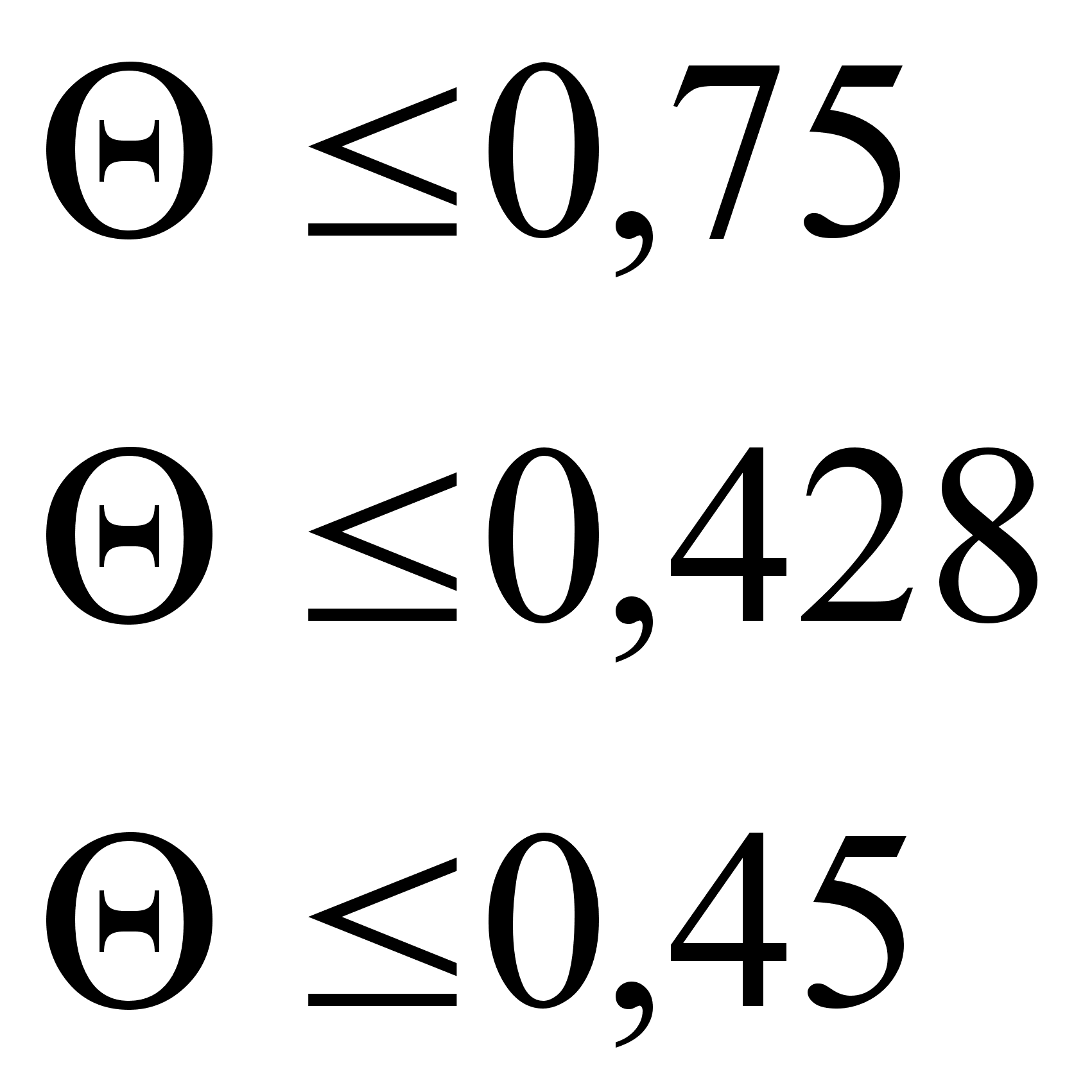
При увеличении ![]() , первой перестает выполнять условие неотрицательности переменная
, первой перестает выполнять условие неотрицательности переменная ![]() , т.к. она первая обращается в ноль. Значит выведем из базиса
, т.к. она первая обращается в ноль. Значит выведем из базиса ![]() . Теперь базисными переменными являются
. Теперь базисными переменными являются ![]() , а свободными
, а свободными ![]() . Для анализа этого плана выразим функцию цели через новые переменные.
. Для анализа этого плана выразим функцию цели через новые переменные.
Из ограничения (2) имеем: ![]() .
.
Подставляя в функцию цели: ![]() получаем:
получаем:
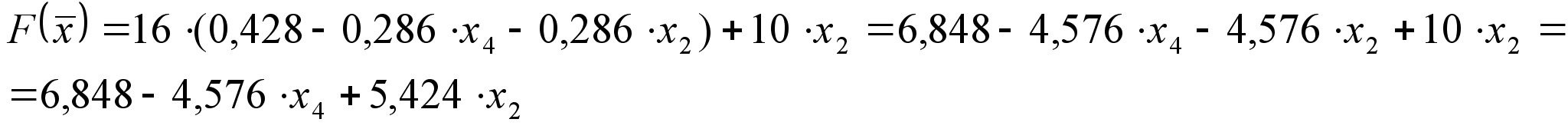
Оформим данный этап задачи в виде симплекс-таблицы:
Начальная симплекс-таблица:
| 16 | 10 | 0 | 0 | 0 | 0 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | в |
| 0 | X3 | 2 | 2 | 1 | 0 | 0 | 0 | 1,5 |
| 0 | X4 | 3,5 | 1 | 0 | 1 | 0 | 0 | 1,5 |
| 0 | X5 | 10 | 4 | 0 | 0 | 1 | 0 | 4,5 |
| 0 | X6 | 0 | 1 | 0 | 0 | 0 | 1 | 0,7 |
| F | -16 | -10 | 0 | 0 | 0 | 0 | 0 | |
![]() ;
;
Пересчитаем элементы исходной таблицы по правилу четырехугольника:
| 16 | 10 | 0 | 0 | 0 | 0 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | В |
| 0 | X3 | 0 | 1,428 | 1 | -0,572 | 0 | 0 | 0,642 |
| 16 | X1 | 1 | 0,286 | 0 | 0,286 | 0 | 0 | 0,428 |
| 0 | X5 | 0 | 1,14 | 0 | -2,86 | 1 | 0 | 0,214 |
| 0 | X6 | 0 | 1 | 0 | 0 | 0 | 1 | 0,7 |
| F | 0 | -5,424 | 0 | 4,576 | 0 | 0 | 6,857 | |
![]() ;
;
Пересчитав все оценки, видим, что ![]() , значит критерий можно улучшить. Будем увеличивать
, значит критерий можно улучшить. Будем увеличивать ![]() . Пусть
. Пусть ![]() , тогда:
, тогда:
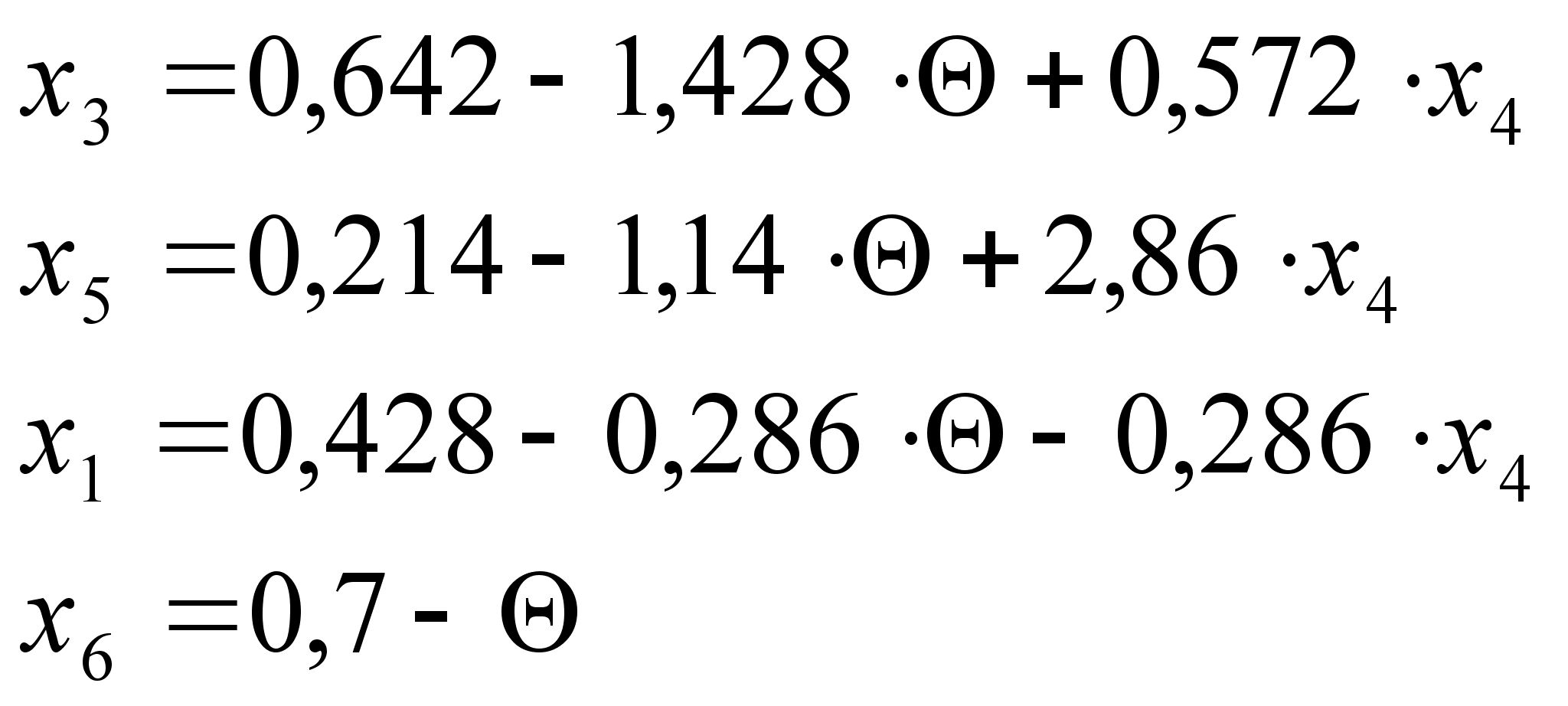
откуда получаем:
![]() ;
;
Все оценки опорного плана должны быть неотрицательны, а значит должны выполняться условия:
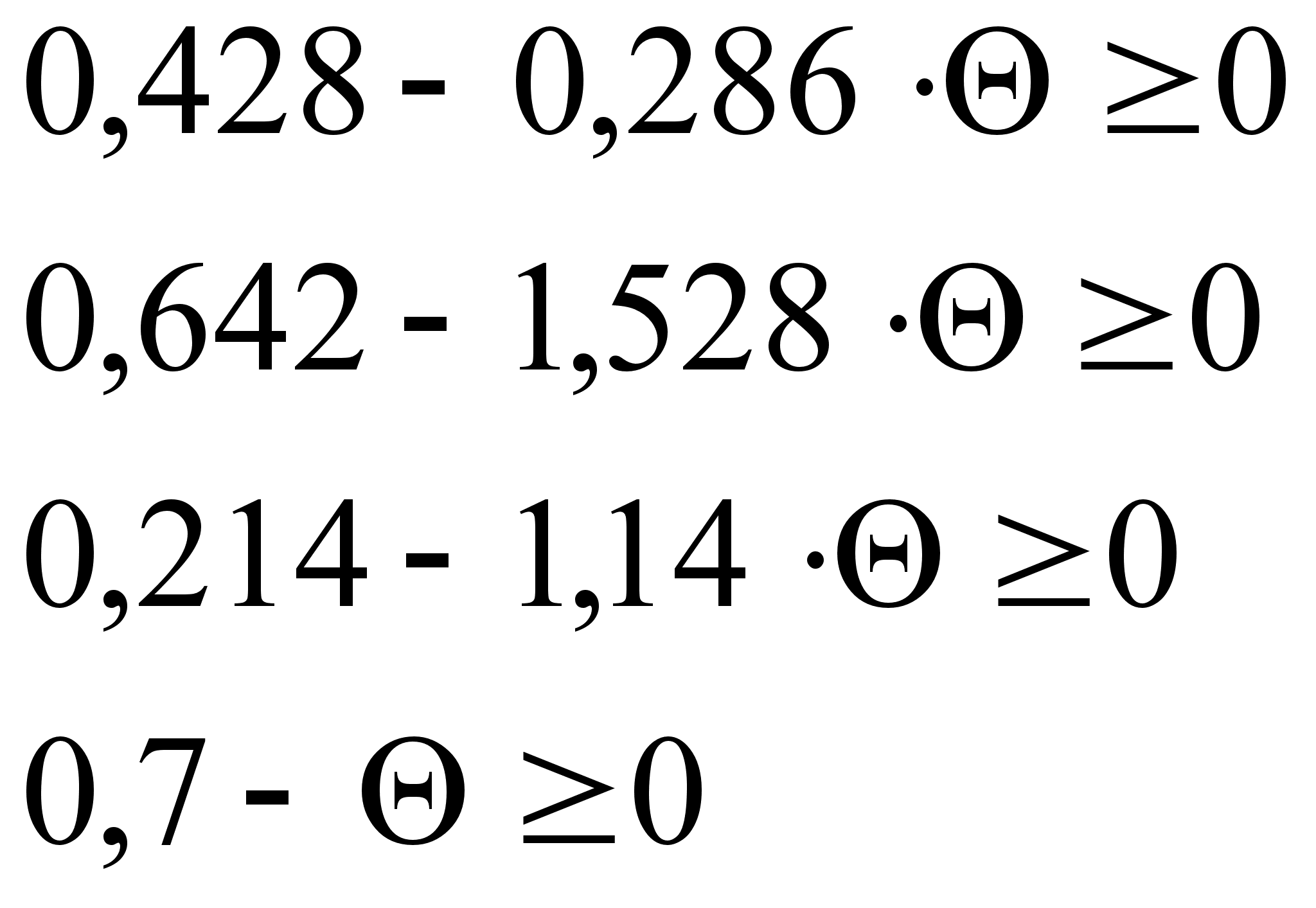 =>
=>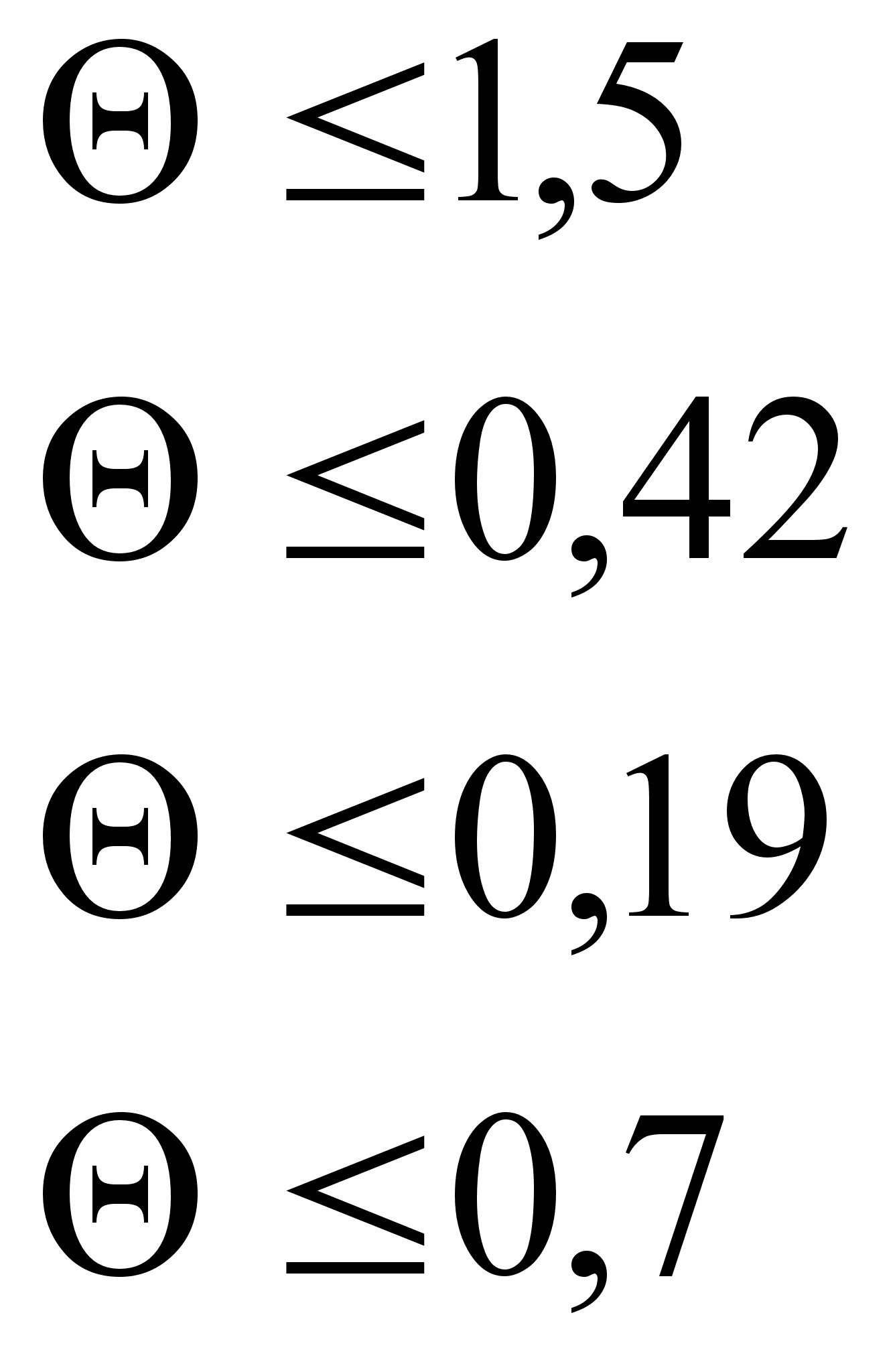
Выведем из базиса ![]() . Теперь базисными переменными являются
. Теперь базисными переменными являются ![]() , а свободными
, а свободными ![]() . Выразим функцию цели через новые переменные:
. Выразим функцию цели через новые переменные:
![]() , а из ограничений (2) и (3):
, а из ограничений (2) и (3): ![]() . Тогда:
. Тогда: ![]() ;
;
16 10 0 0 0 0 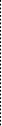 Св
СвБ.П. X1
X2
X3
X4
X5
X6
В 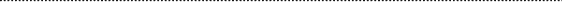 0
0X3
0 0 1 3 -1,25 0 0,375 16 X1
1 0 0 1 -0,25 0 0,375 10 X2
0 1 0 -2,5 0,875 0 0,1875 0 X6
0 0 0 2,5 -0,875 1 0,5125 F 0 0 0 -9 4,75 0 7,875
![]()
Пересчитав все оценки, видим, что ![]() , значит критерий можно улучшить. Будем увеличивать
, значит критерий можно улучшить. Будем увеличивать ![]() . Пусть
. Пусть ![]() , тогда:
, тогда:
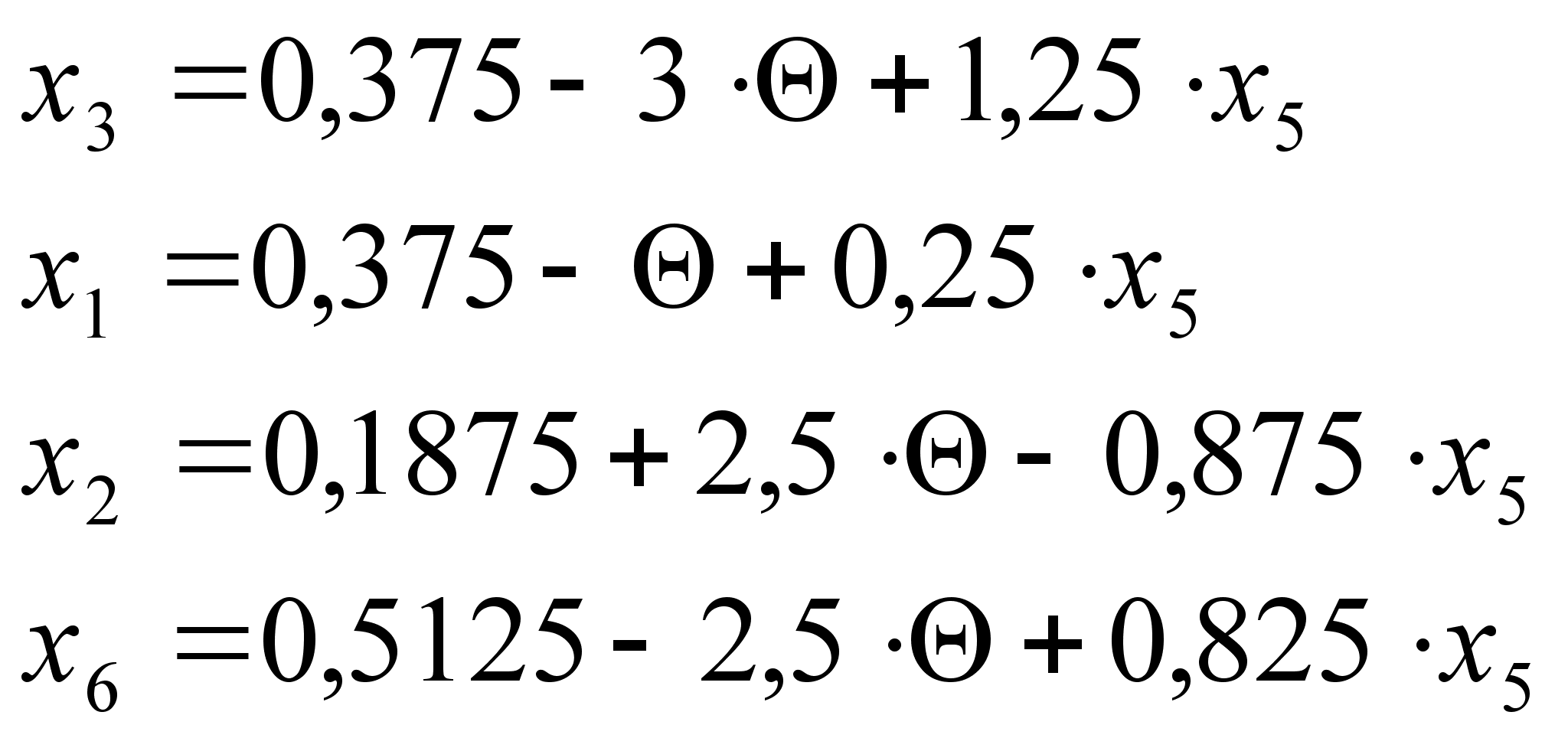
откуда получаем:
![]() ;
;
Все оценки опорного плана должны быть неотрицательны, а значит должны выполняться условия:
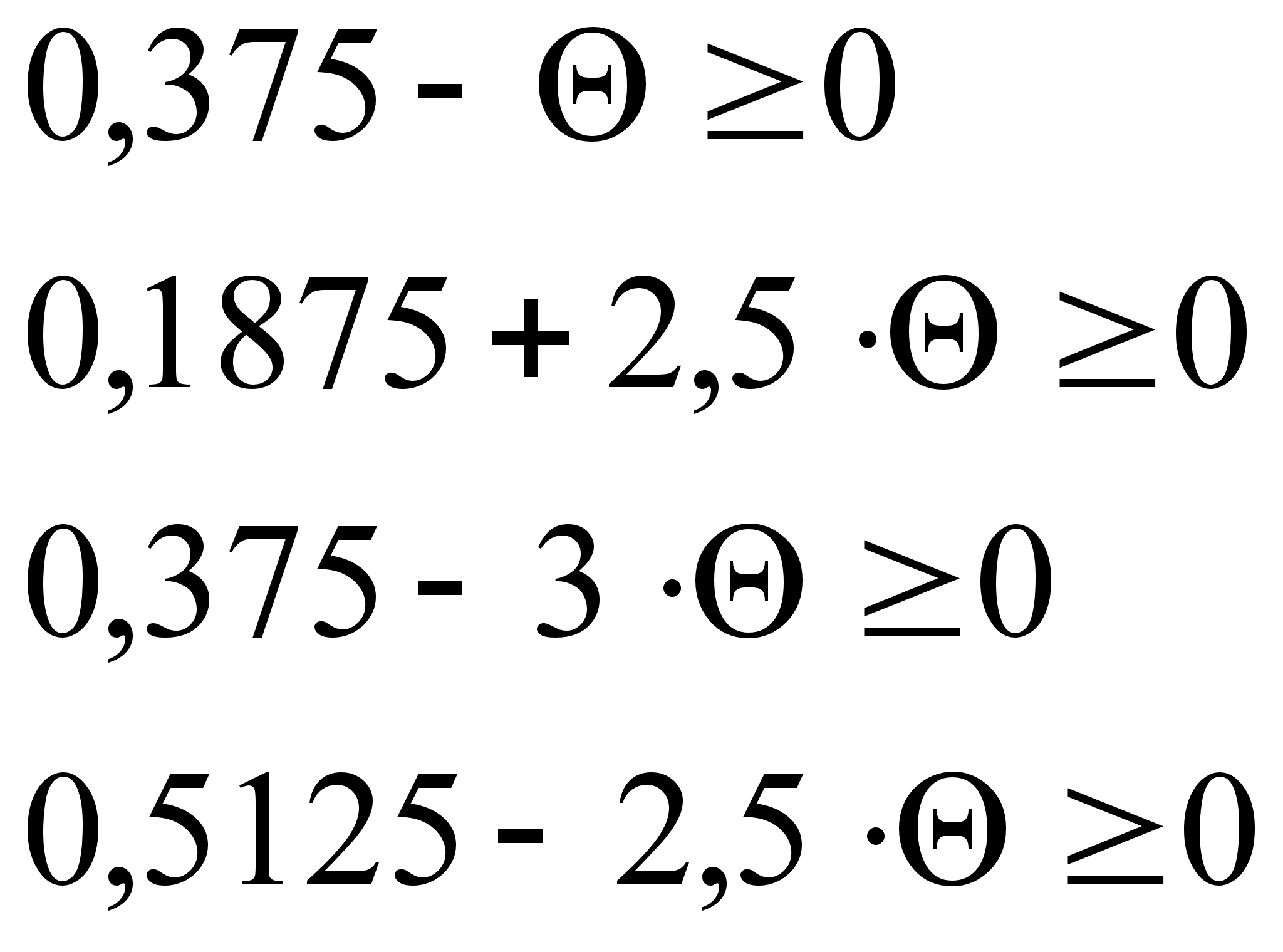 =>
=>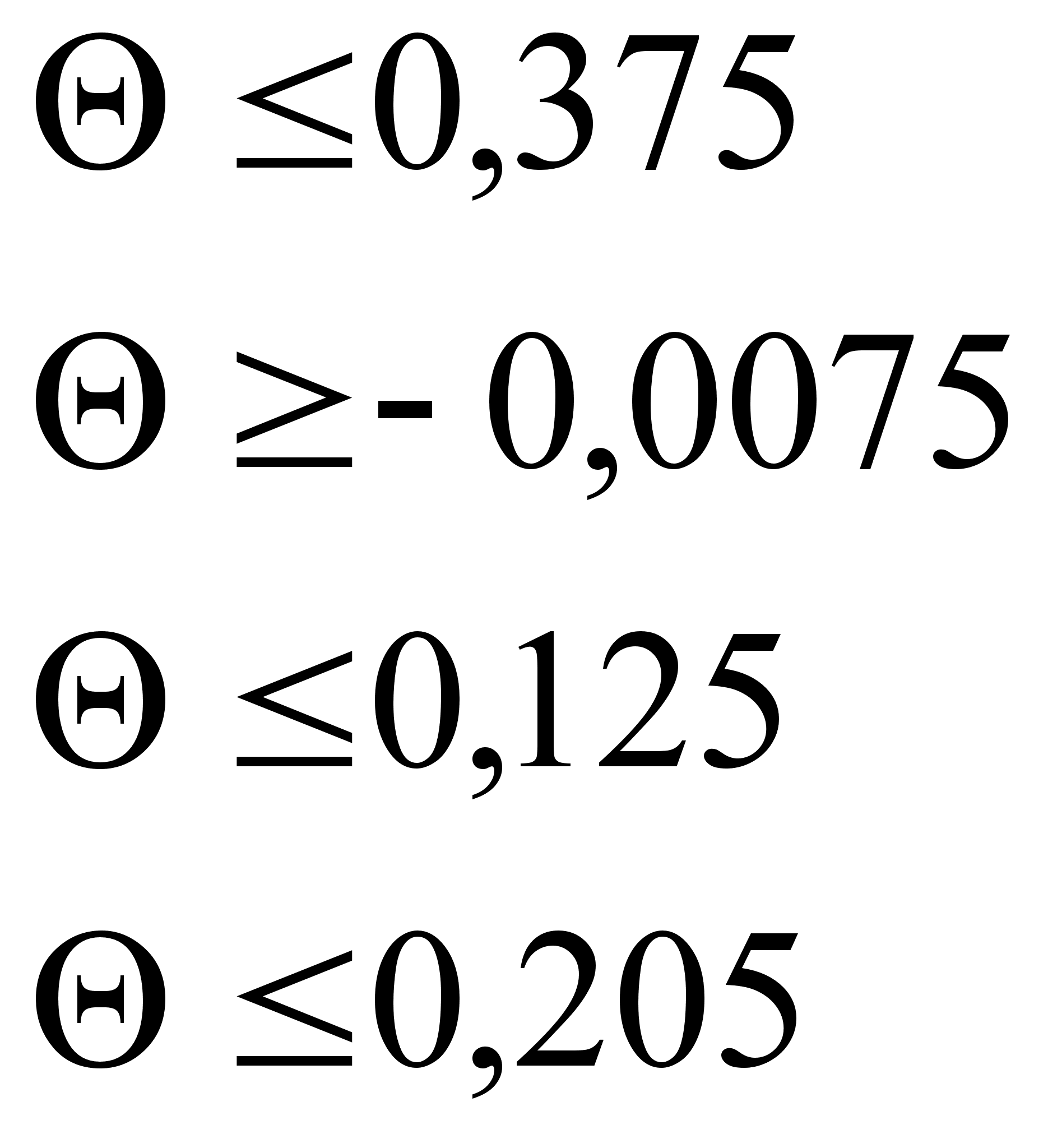
Выведем из базиса ![]() . Теперь базисными переменными являются
. Теперь базисными переменными являются ![]() , а свободными
, а свободными ![]() . Выразим функцию цели через новые переменные:
. Выразим функцию цели через новые переменные:
![]() , а из ограничений (1) и (2):
, а из ограничений (1) и (2): ![]() . Тогда:
. Тогда: ![]() ;
;
16 10 0 0 0 0 Св
Б.П. X1
X2
X3
X4
X5
X6
в 0 X4
0 0 0,333 1 -0,416 0 0,125 16 X1
1 0 -0,333 0 0,166 0 0,25 10 X2
0 1 1,833 0 -0,166 0 0,5 0 X6
0 0 -0,833 0 0,166 1 0,2 F 0 0 3 0 1 0 9
![]()
Видим, что все оценки положительны, значит любое увеличение какой-либо свободной переменной уменьшит критерий. Данное решение является оптимальным. Изобразим это решение на графике:
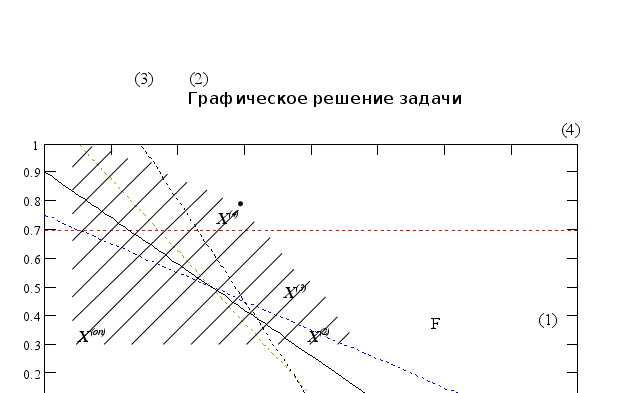
Видим, что ![]() единственное и достигается в угловой точке области допустимых решений.
единственное и достигается в угловой точке области допустимых решений.
2 вариант.
Отмечая успешно сданную сессию, вышеупомянутые студенты взяли столько же пива и в таких же пропорциях, за исключением того, что вместо пива «Премьер» было куплено пиво «Окское», крепость которого 6,4 % (дешевое и разбавленное). Определить план распития напитков для получения максимального суммарного опьянения (в ![]() ).
).
Функция цели: ![]() .
.
Приводим ограничения к каноническому виду:
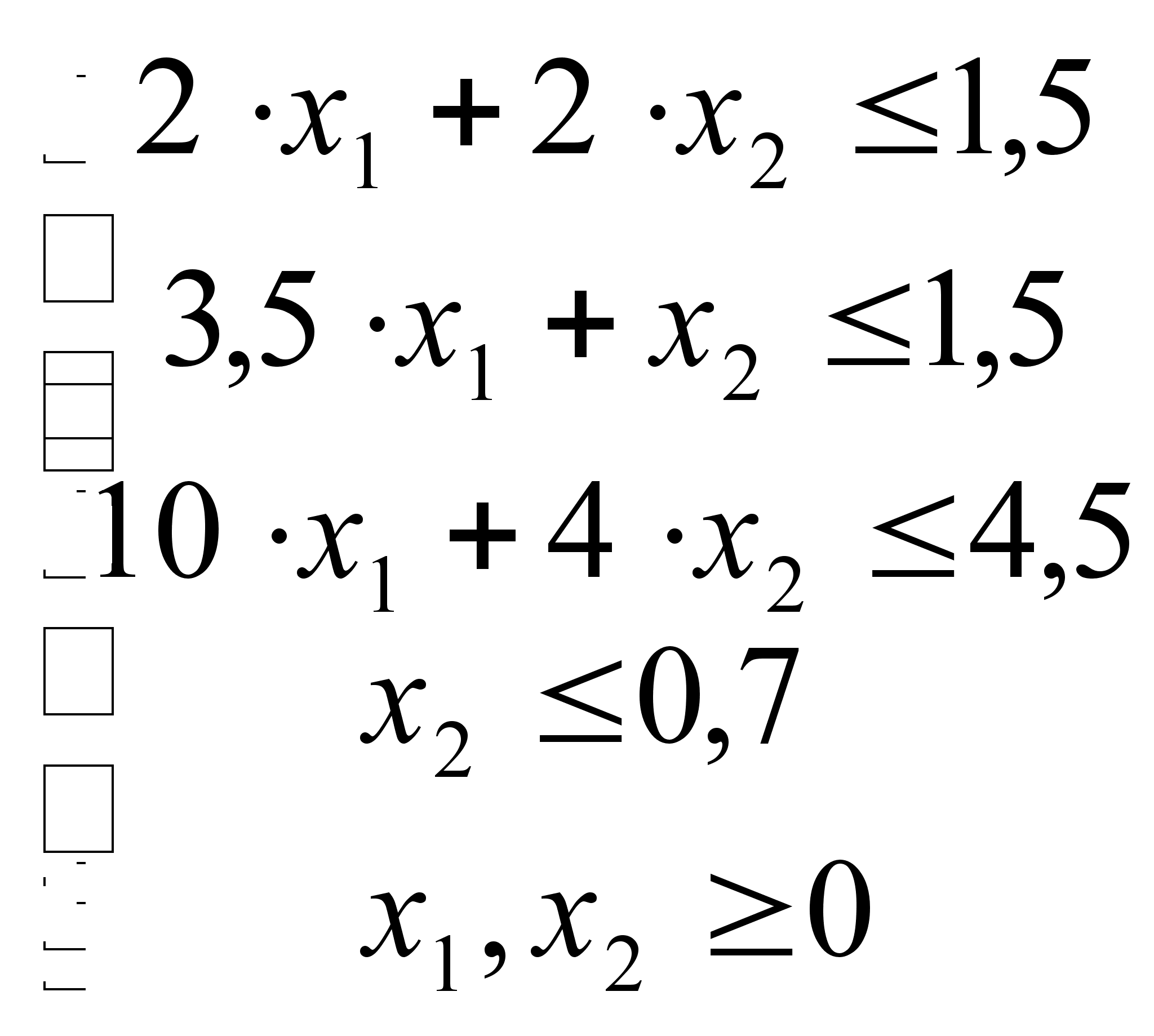
![]() =>
=>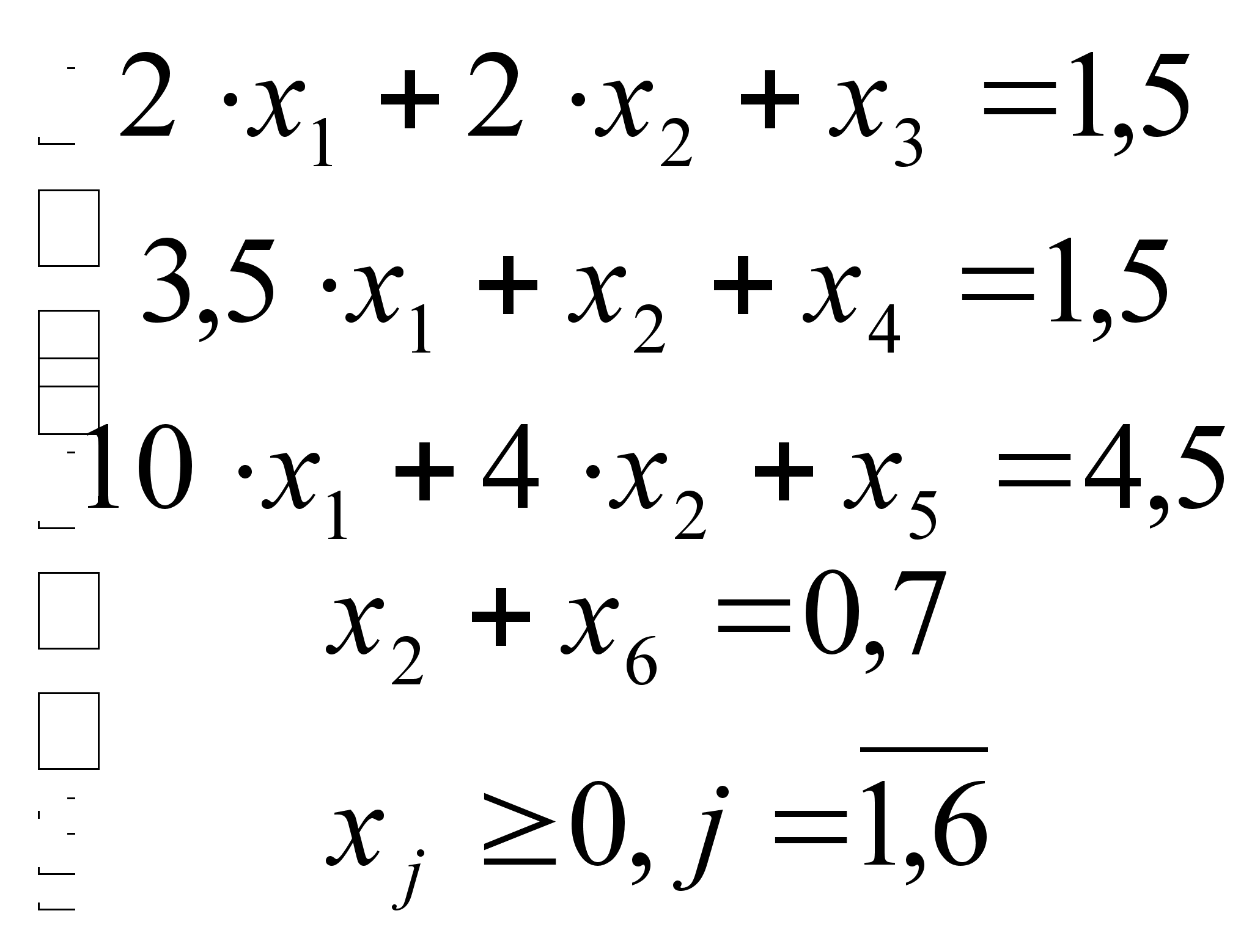
![]()
Решаем симплекс-методом:
16 6,4 0 0 0 0  Св
СвБ.П. X1
X2
X3
X4
X5
X6
В 0 X3
2 2 1 0 0 0 1,5 0 X4
3,5 1 0 1 0 0 1,5 0 X5
10 4 0 0 1 0 4,5 0 X6
0 1 0 0 0 1 0,7 F -16 -10 0 0 0 0 0
![]() ,
, ![]()
16 6,4 0 0 0 0  Св
СвБ.П. X1
X2
X3
X4
X5
X6
В 0 X3
0 1,428 1 -0,571 0 0 0,642 16 X1
1 1,286 0 0,286 0 0 0,428 0 X5
0 1,142 0 -2,85 1 0 0,214 0 X6
0 1 0 0 0 1 0,7 F 0 -1,82 0 4,571 0 0 6,857
![]() ;
; ![]()
16 6,4 0 0 0 0 Св
Б.П. X1
X2
X3
X4
X5
X6
В 0 X3
0 0 1 3 -1,25 0 0,375 16 X1
1 0 0 1 -0,25 0 0,375 6,4 X2
0 1 0 -2,5 0,875 0 0,1875 0 X6
0 0 0 2,5 -0,875 1 0,5125 F 0 0 0 0 1,6 0 7,2
![]() ;
; ![]()
Видим, что все оценки положительны, значит оптимальное решение достигнуто. Но одна из свободных переменных (![]() ) обратилась в ноль, и если мы ее будем увеличивать, то функция цели не изменится, а решение будет другим, т.е. получим еще одно оптимальное решение, которое будет называться альтернативным.
) обратилась в ноль, и если мы ее будем увеличивать, то функция цели не изменится, а решение будет другим, т.е. получим еще одно оптимальное решение, которое будет называться альтернативным.
16 10 0 0 0 0 Св
Б.П. X1
X2
X3
X4
X5
X6
в 0 X4
0 0 0,333 1 -0,416 0 0,125 16 X1
1 0 -0,333 0 0,166 0 0,25 10 X2
0 1 1,833 0 -0,166 0 0,5 0 X6
0 0 -0,833 0 0,166 1 0,2 F 0 0 0 0 1 0 7,2
![]()
Если оптимальное решение достигнуто в 2-х точках, то оно достигается и на отрезке между ними. Можно составить уравнение данного отрезка по формуле:
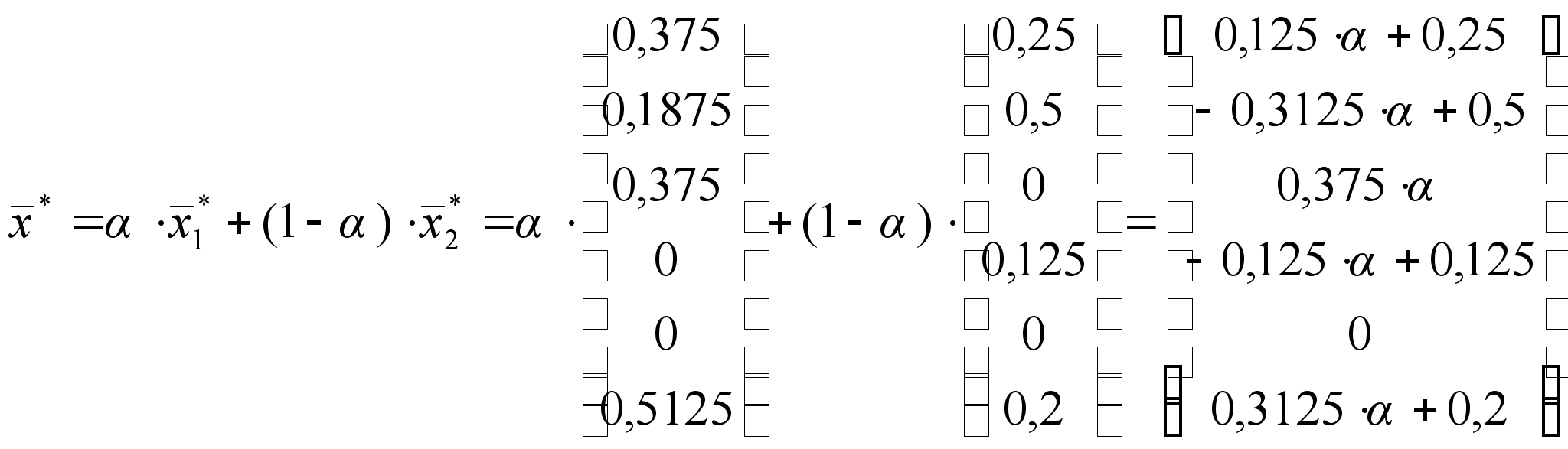 ;
;
![]() ;
;
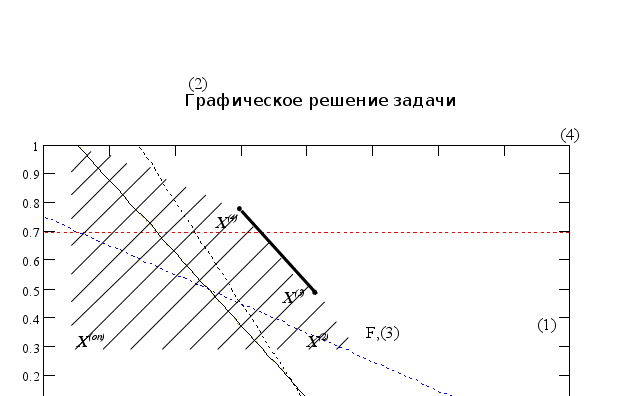
На графике видно, что оптимальное решение достигается на отрезке, значит является альтернативным. Вектор градиента целевой функции (F) параллелен радиус-вектору ограничения (3). Это ограничение образует все множество оптимальных решений.
Можно сделать вывод, что альтернативные решения имеются, когда все оценки свободных переменных больше 0, а среди коэффициентов целевой функции оценка одной из свободных переменных равна 0.
3 вариант.
Студент Петров, решив догнать по количеству выпитого студента Сидорова, выпил 4 доли пива «Русич» вместо запланированных 3,5. Решим задачу с учетом изменившихся данных.
Функция цели:![]() .
.
Приводим ограничения к каноническому виду:
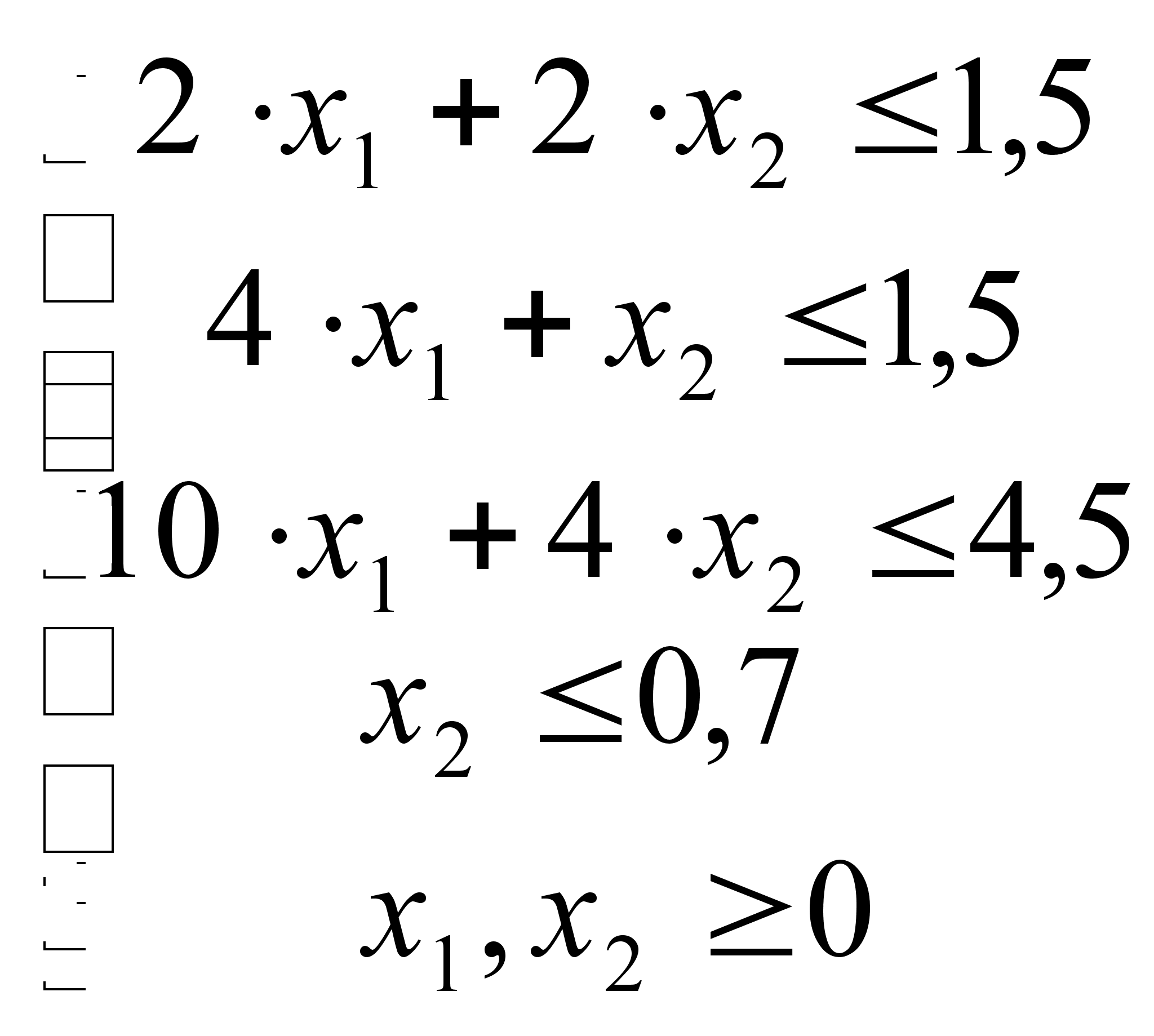
![]() =>
=>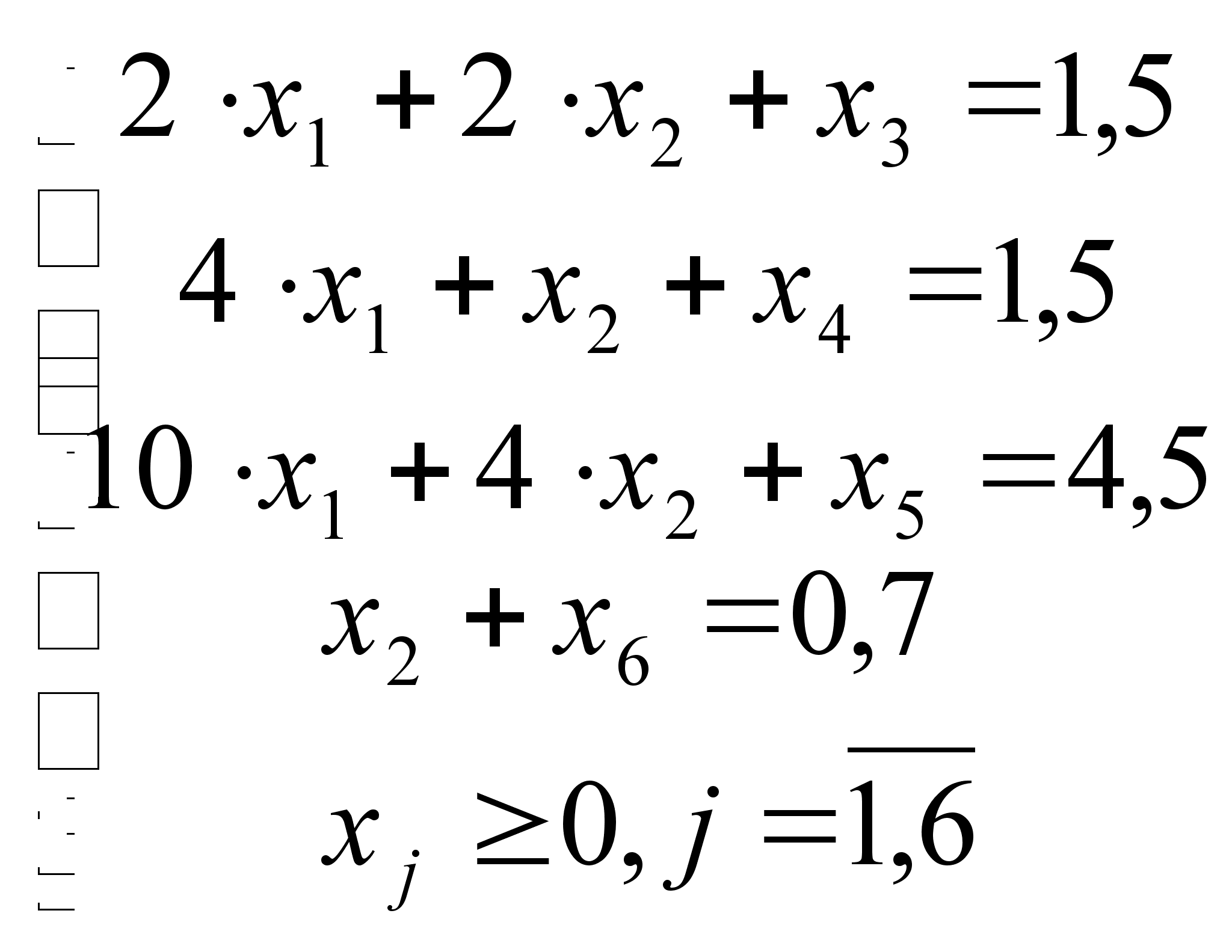
![]()
Решим задачу симплекс-методом.
| 16 | 10 | 0 | 0 | 0 | 0 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | в |
| 0 | X3 | 2 | 2 | 1 | 0 | 0 | 0 | 1,5 |
| 0 | X4 | 4 | 1 | 0 | 1 | 0 | 0 | 1,5 |
| 0 | X5 | 10 | 4 | 0 | 0 | 1 | 0 | 4,5 |
| 0 | X6 | 0 | 1 | 0 | 0 | 0 | 1 | 0,7 |
| F | -16 | -10 | 0 | 0 | 0 | 0 | 0 | |
![]() ,
, ![]() .
.
| 16 | 10 | 0 | 0 | 0 | 0 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | В |
| 0 | X3 | 0 | 1,5 | 1 | -0,5 | 0 | 0 | 0,75 |
| 16 | X1 | 1 | 0,25 | 0 | 0,25 | 0 | 0 | 0,375 |
| 0 | X5 | 0 | 1,5 | 0 | -2,5 | 1 | 0 | 0,75 |
| 0 | X6 | 0 | 1 | 0 | 0 | 0 | 1 | 0,7 |
| F | 0 | -6 | 0 | 4 | 0 | 0 | 6 | |
![]() ,
, ![]() .
.
| 16 | 10 | 0 | 0 | 0 | 0 | |||
Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | в |
| 10 | X2 | 0 | 1 | 1,666 | -0,333 | 0 | 0 | 0,5 |
| 16 | X1 | 1 | 0 | -0,166 | 0,333 | 0 | 0 | 0,25 |
| 0 | X5 | 0 | 0 | -1 | -2 | 1 | 0 | 0 |
| 0 | X6 | 0 | 0 | -0,666 | 0,333 | 0 | 1 | 0,2 |
| F | 0 | 0 | 4 | 2 | 0 | 0 | 9 | |
![]() ,
, ![]()
Данное оптимальное решение является вырожденным, т.к. положительных компонентов меньше числа ограничений. На существование вырожденного оптимального решения указывает наличие в симплекс-таблице нулевого свободного члена при найденном оптимальном решении.
В случае вырожденного решения симплекс-таблица может зацикливаться. Существует 2 способа предупреждения зацикливания:
а) ![]() – изменение хода ограничения на некоторые величины
– изменение хода ограничения на некоторые величины ![]() . Они должны быть малы, чтобы изменения были несущественны.
. Они должны быть малы, чтобы изменения были несущественны.
б) Если минимальное отношение свободных коэффициентов к положительным членам разрешающего столбца определяется неоднозначно, то выбирается отношение любого другого столбца к положительным коэффициентам данного столбца, пока строка не определится однозначно.

4 вариант.
В связи с неожиданно полученной стипендией, запасы пива резко увеличились.
Функция цели: ![]() .
.
Приводим ограничения к каноническому виду:
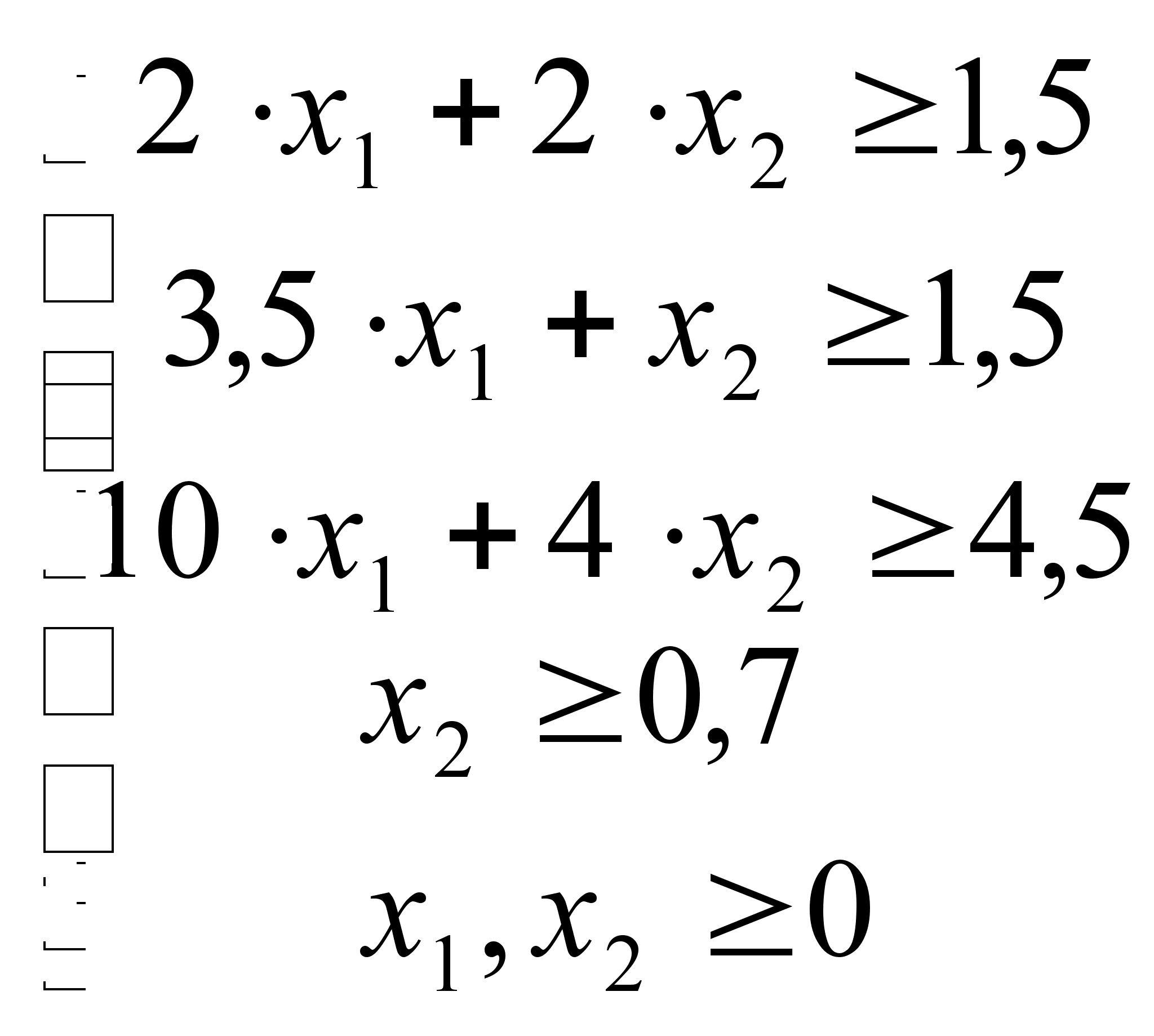
![]() =>
=>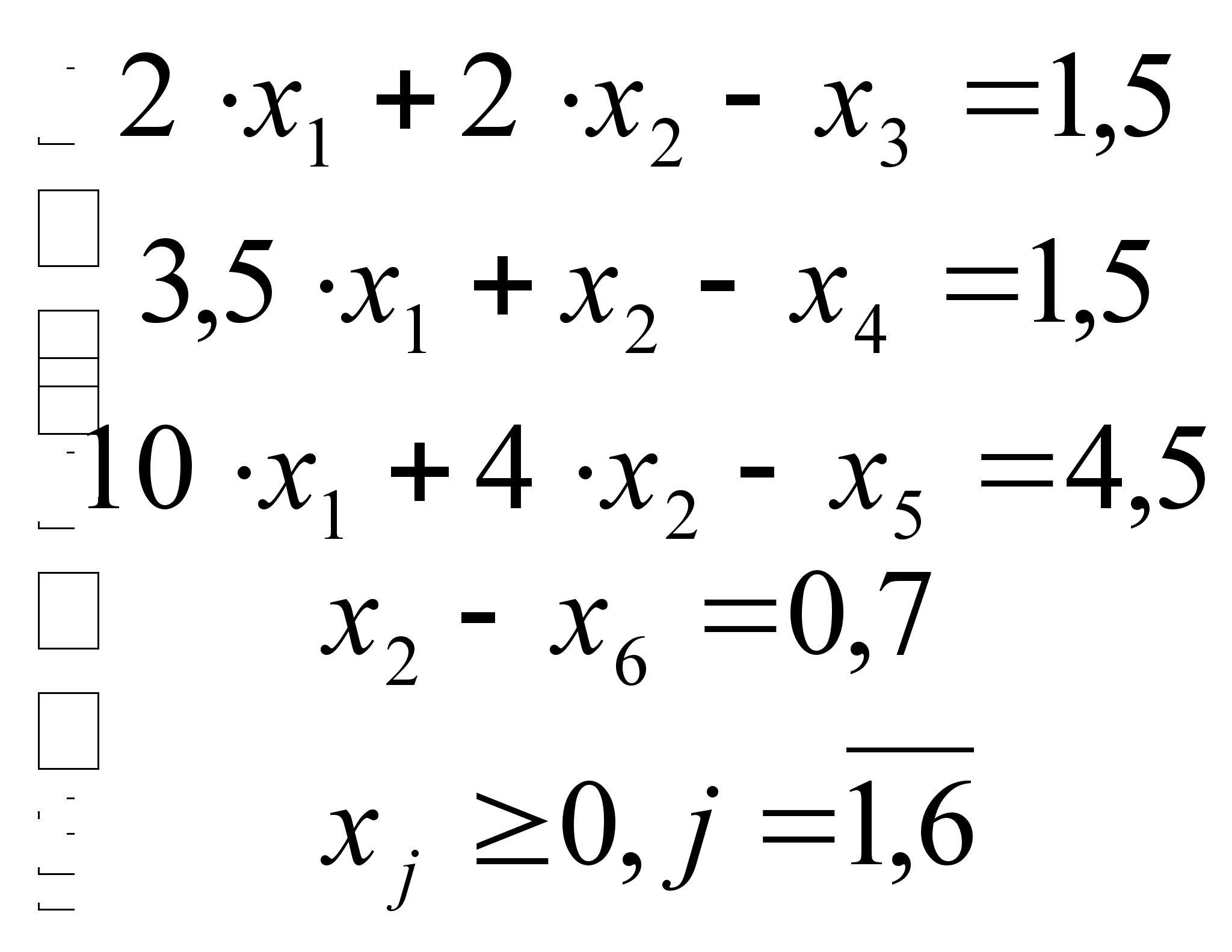
![]()
В матрице условий нет единичной подматрицы, поэтому используем метод искусственного базиса. Построим вспомогательную задачу.
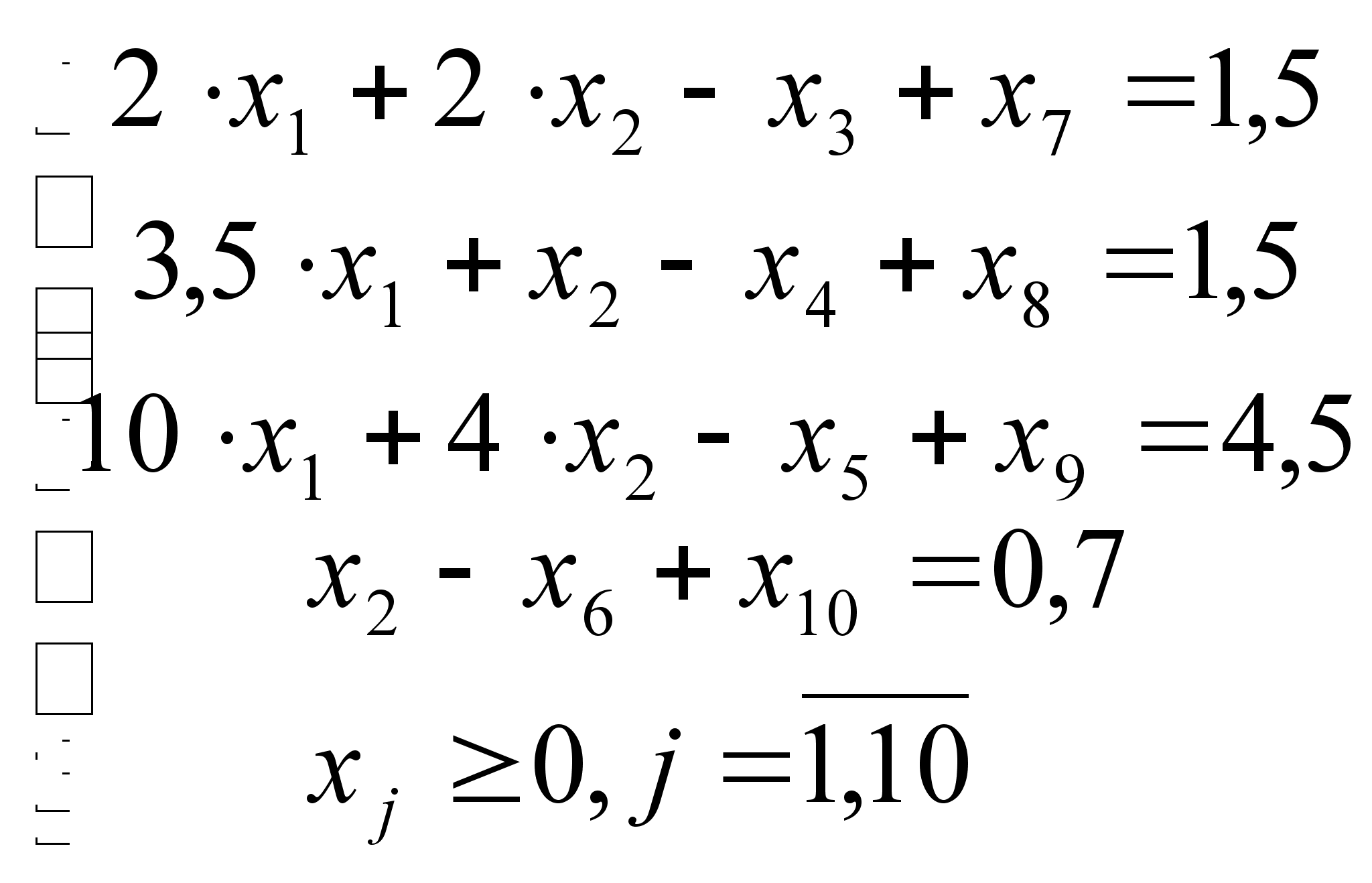
![]() , при этом
, при этом ![]() .
.
Решаем вспомогательную задачу симплекс-методом:
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | в |
| 1 | X7 | 2 | 2 | -1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1,5 |
| 1 | X8 | 3.5 | 1 | 0 | -1 | 0 | 0 | 0 | 1 | 0 | 0 | 1,5 |
| 1 | X9 | 10 | 4 | 0 | 0 | -1 | 0 | 0 | 0 | 1 | 0 | 4,5 |
| 1 | X10 | 0 | 1 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 1 | 0,7 |
| F | 15,5 | 8 | -1 | -1 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | в |
| 1 | X7 | 0 | 1,428 | -1 | 0,571 | 0 | 0 | 1 | -0,571 | 0 | 0 | 0,642 |
| 0 | X1 | 1 | 0,285 | 0 | -0,285 | 0 | 0 | 0 | 0,285 | 0 | 0 | 0,428 |
| 1 | X9 | 0 | 1,142 | 0 | 2,857 | -1 | 0 | 0 | -2,85 | 1 | 0 | 0,214 |
| 1 | X10 | 0 | 1 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 1 | 0,7 |
| F | 0 | 3.571 | -1 | 3,428 | -1 | -1 | 0 | -4,42 | 0 | 0 | 1,557 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | в |
| 1 | X7 | 0 | 0 | -1 | -3 | 1,25 | 0 | 1 | 3 | -1,25 | 0 | 0,375 |
| 0 | X1 | 1 | 0 | 0 | -1 | 0,25 | 0 | 0 | 1 | -0,25 | 0 | 0,375 |
| 0 | X2 | 0 | 1 | 0 | 2,5 | -0,875 | 0 | 0 | -2,5 | 0,875 | 0 | 0,187 |
| 1 | X10 | 0 | 0 | 0 | -2,5 | 0,875 | -1 | 0 | 2,5 | -0,875 | 1 | 0,512 |
| F | 0 | 0 | -1 | -5,5 | 2,125 | -1 | 0 | 4,5 | -3,12 | 0 | 0,887 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | в |
| 1 | X8 | 0 | 0 | -0,333 | -1 | 0,416 | 0 | 0,333 | 1 | -0,416 | 0 | 0,125 |
| 0 | X1 | 1 | 0 | 0,333 | 0 | -0,166 | 0 | -,333 | 0 | 0,166 | 0 | 0,25 |
| 0 | X2 | 0 | 1 | -0,833 | 0 | 0,166 | 0 | 0,833 | 0 | -0,166 | 0 | 0,5 |
| 1 | X10 | 0 | 0 | 0,833 | 0 | -0,166 | -1 | -0,833 | 0 | 0,166 | 1 | 0,2 |
| F | 0 | 0 | 0,5 | -1 | 0,25 | -1 | -1,5 | 0 | -1,25 | 0 | 0,325 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
| Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | в |
| 1 | X8 | 0 | 0 | 0 | -1 | 0,35 | -0,4 | 0 | 1 | -0,35 | 0,4 | 0,205 |
| 0 | X1 | 1 | 0 | 0 | 0 | -0,1 | 0,4 | 0 | 0 | 0,1 | -0,4 | 0,17 |
| 0 | X2 | 0 | 1 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 1 | 0,7 |
| 0 | X3 | 0 | 0 | 1 | 0 | -0,2 | -1,2 | -1 | 0 | 0,2 | 1,2 | 0,24 |
| F | 0 | 0 | 0 | -1 | 0,35 | -0,4 | -1 | 0 | -1,35 | -0,6 | 0,205 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | в |
| 0 | X5 | 0 | 0 | 0 | -2,85 | 1 | -1,14 | 0 | 2,857 | -1 | -1,142 | 0,585 |
| 0 | X1 | 1 | 0 | 0 | -0,285 | 0 | 0,285 | 0 | 0,285 | 0 | -0,285 | 0,228 |
| 0 | X2 | 0 | 1 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 1 | 0,7 |
| 0 | X3 | 0 | 0 | 1 | -0,571 | 0 | -1,42 | -1 | -1,571 | 0 | 1,428 | 0,357 |
| F | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | 0 | |
![]() – оптимальное решение вспомогательной задачи. Искусственные переменные являются свободными и равны нулю. Т.о. это решение является опорным планом исходной задачи.
– оптимальное решение вспомогательной задачи. Искусственные переменные являются свободными и равны нулю. Т.о. это решение является опорным планом исходной задачи.
Решим исходную задачу:
16 10 0 0 0 0 Св
Б.П. X1
X2
X3
X4
X5
X6
в 0 X5
0 0 0 -2,85 1 -1,14 0,585 16 X1
1 0 0 -0,285 0 0,285 0,228 10 X2
0 1 0 0 0 -1 0,7 0 X3
0 0 1 -0,571 0 -1,42 0,357 F 0 0 0 -4,576 0 -5,424 3,648
К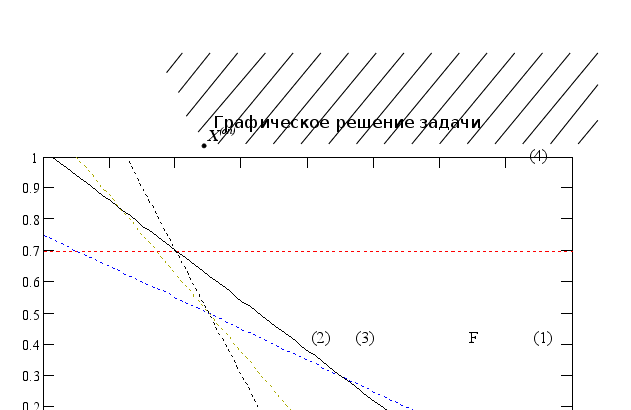 ритерий можно улучшить, т.к.
ритерий можно улучшить, т.к. ![]() ,
, ![]() , но нельзя найти такое
, но нельзя найти такое ![]() , при котором базисные переменные обращаются в 0. Значит задача неразрешима из-за неограниченности критерия.
, при котором базисные переменные обращаются в 0. Значит задача неразрешима из-за неограниченности критерия.
5 вариант.
После отмеченного таким образом праздника обязательно наступает похмелье. Решим задачу из предыдущего варианта, минимизируя этот неприятный фактор, т.е. функция цели: ![]() .
.
Приводим ограничения к каноническому виду:
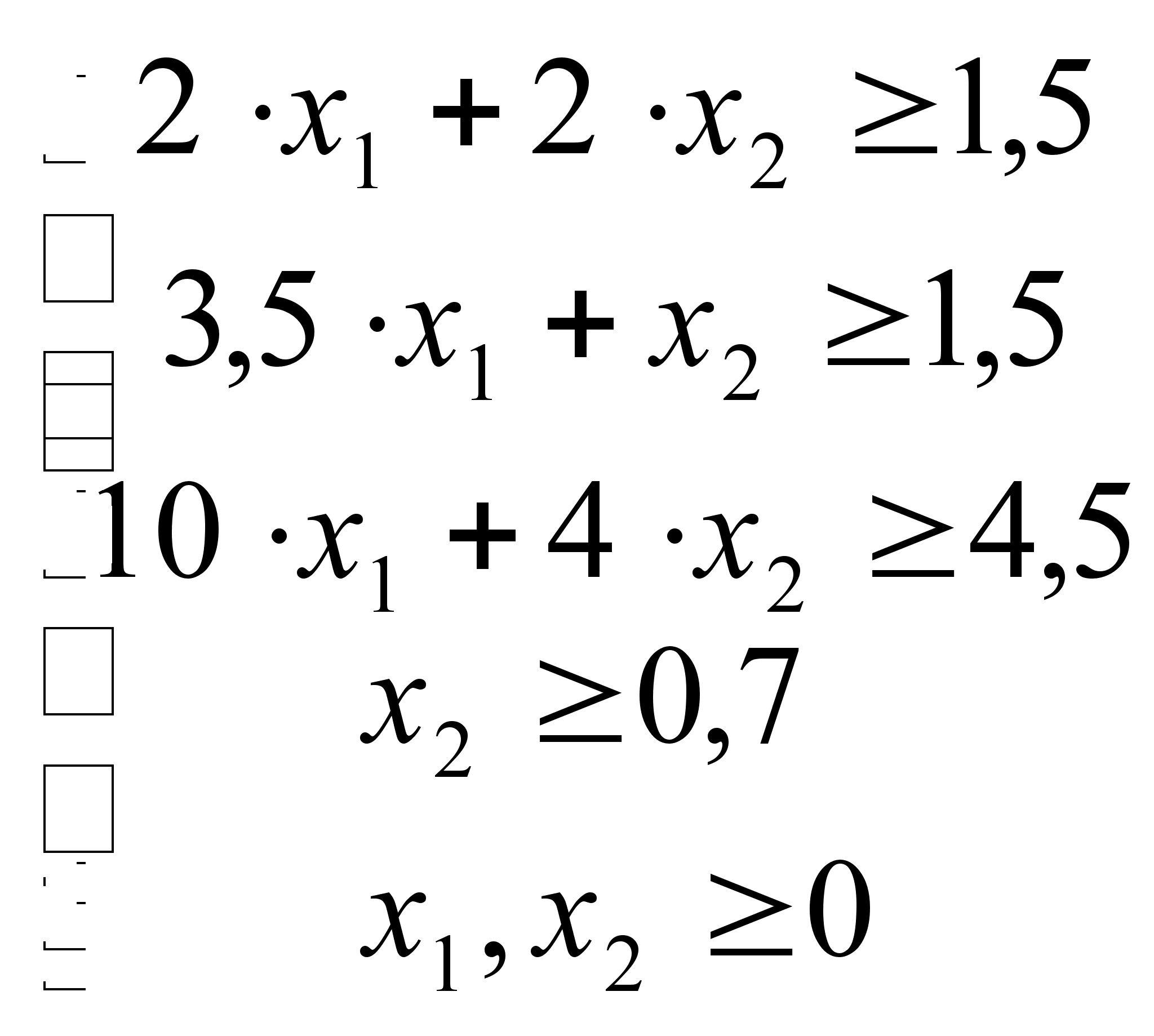
![]() =>
=>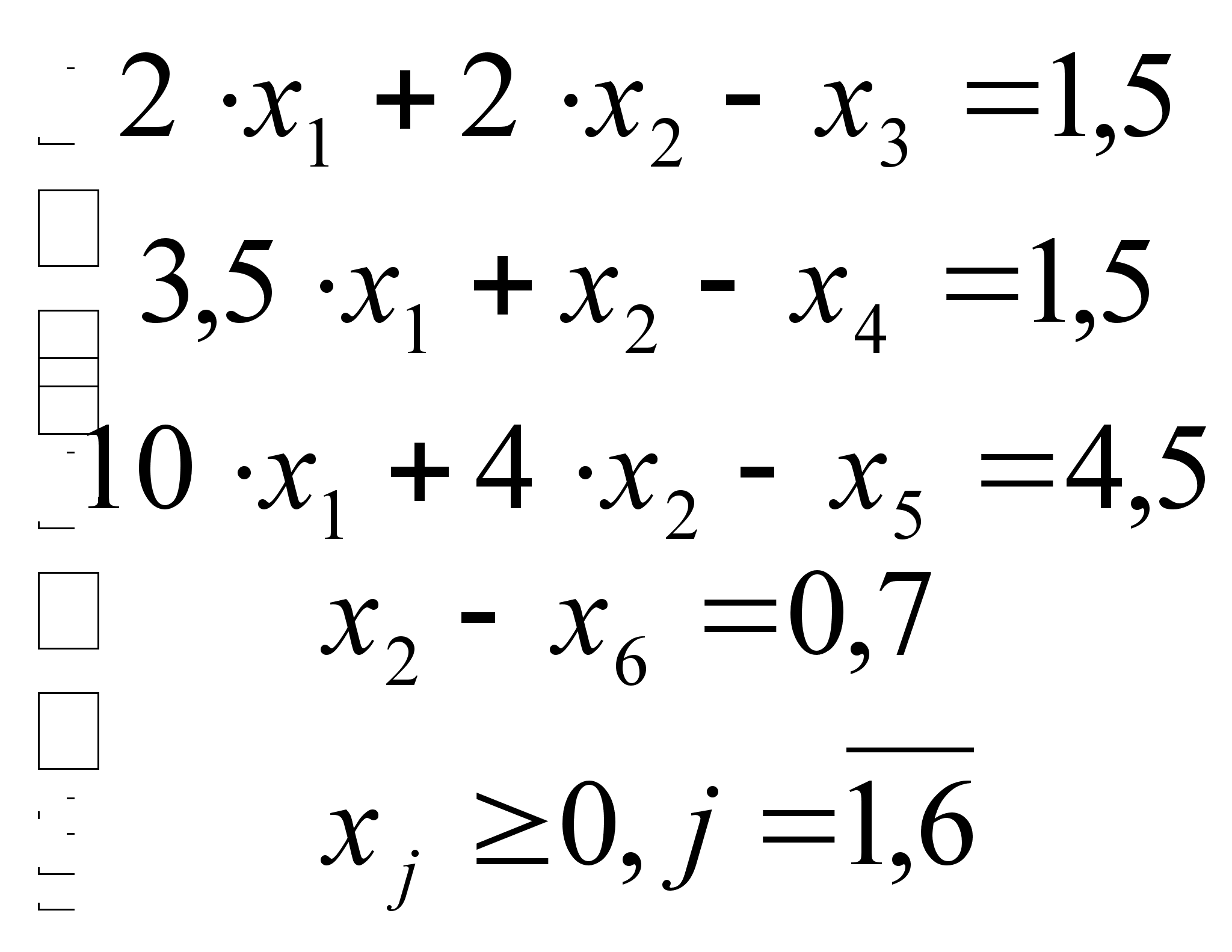
![]()
Эта задача решается методом искусственного базиса, т.к. в ней нет единичной подматрицы. Вспомогательная задача получается точно такой же, как и в предыдущем варианте, поэтому просто возьмем опорный план из предыдущей задачи.
![]() ;
;
16 10 0 0 0 0 Св
Б.П. X1
X2
X3
X4
X5
X6
в 0 X5
0 0 0 -2,85 1 -1,14 0,585 16 X1
1 0 0 -0,285 0 0,285 0,228 10 X2
0 1 0 0 0 -1 0,7 0 X3
0 0 1 -0,571 0 -1,42 0,357 F 0 0 0 -4,576 0 -5,424 3,648
Видим, что оценки свободных переменных меньше нуля, значит решение оптимальное.
![]() ; F = 3,648.
; F = 3,648.
Д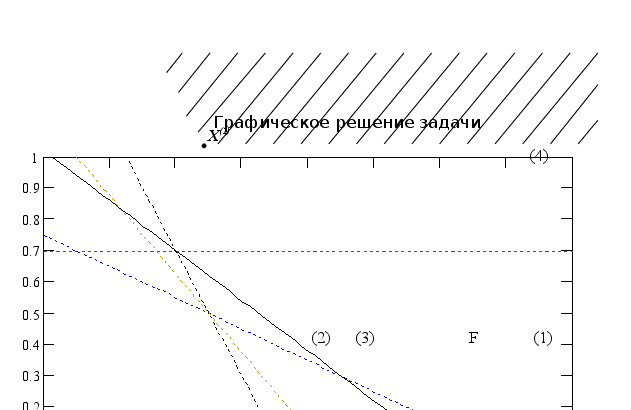 елаем вывод: оптимальное решение может существовать и при неограниченности области.
елаем вывод: оптимальное решение может существовать и при неограниченности области.
Область не ограничена, но существует оптимальное решение ![]() , причем единственное, которое достигается в угловой точке.
, причем единственное, которое достигается в угловой точке.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Лекции (1-18) по мат. анализу 1 семестр
По всем вопросам и по дальнейшему пополнению лекций обращаться на ящикvan_mo_mail@mtu-net.ruили на сотовый:8-901-7271056 спросить Ваню екция №1 Вед
- Лекции переходящие в шпоры Алгебра и геометрия
1. Матрицы. Терминология и обозначения.Матрицей размера (mxn) называется набор m×n чисел – элементов м-цы Ai,j, записанных в виде прямоугол
- Лекции по Математическому анализу
Аксиоматика вещественных чисел. Алгебраические свойства вещественных чисел. На множестве вещественных чисел определена операция слож
- Лекции по матану (III семестр) переходящие в шпоры
1 Двойной интегралРассмотрим в плоскости Оху замкнутую область D, ограниченную линией Г, являющейся замкнутой непрерывной кривой. z = l(P) =
- Линейное и динамическое программирование
Линейное программирование.Задача линейного оптимального планирования - один из важнейших математических инструментов, используемых в
- Линейное программирование: постановка задач и графическое решение
Линейное программирование - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвес
- Лобачевский и неевклидова геометрия
Сигулдская средняя школа N2Кронвальда 7, Сигулда, ЛатвияНеевклидова геометрия.Проект ученика 11а класса Чиркова АндреяКонсультант: Степу
Copyright © https://referat-web.com/. All Rights Reserved
 www.referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
www.referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.


 Св
Св Св
Св Св
Св Св
Св Св
Св Св
Св Св
Св