Скачать

Оптимизация расстановки транспортных средств на открытых автостоянках в интересах Государственной противопожарной службы

За последние несколько лет увеличилось количество автомобильного транспорта, поэтому на сегодняшний день существует острейшая проблема временного и постоянного хранения автотранспорта в условиях крупных городов, в местах интенсивных людских потоков, таких как центральная часть города, железнодорожные вокзалы, торговые комплексы, а также деловые центры и жилой сектор города. Следовательно, можно сделать простой вывод: парковка автомобиля – одна из актуальных проблем сегодня.

Транспортные трудности, в том числе вся возрастающая потребность в стоянках транспортных средств, на разных этапах развития решались при помощи некоторых иерархических систем. Нехватка места для автомобилей подтверждается простым расчетом. Стоящий автомобиль с учетом подъездов к нему занимает около 25 , едущий с учетом динамического габарита около 40 . Среднее число пассажиров в индивидуальном автомобиле 1.2-1.6 человек. Известно, что в общегородском центре одновременно бывает около 10-15 % всего населения города. Если каждый будет приезжать на автомобиле, то в центре города с миллионным населением могут искать места около 120 тысяч автомобилей. Для них потребовалось бы:

120.00025=3.000.000  или 300 гектаров, или 3  территории (7).

Трудности размещения стоящих автомобилей начинаются на разных стадиях автомобилизации. Процесс паркирования автомобилей имеет специфические особенности. Среди них следует упомянуть трудности выделения территории для стоящего транспорта, взаимодействия стоянок с другими элементами города, обеспечения охраны окружающей среды, безопасности движения. Очень многое зависит от общей культуры, сознательности владельцев и водителей автомобилей. Добровольный отказ от излишнего шума при погрузке, разгрузке, высадке, посадке, приготовлении автомобиля к поездке, применении сигнализации, учет требовании времени отдыха людей в жилых районах могут помочь решить проблемы паркирования, сделать стоянки удобными как для владельцев автомобилей, так и для жителей районов. При решении этих вопросов необходимо взаимопонимание.

Автомобильную стоянку необходимо считать системой, удовлетворяющей спрос на паркирование транспортных средств, которая располагает ограниченными возможностями удовлетворения этого спроса. Поэтому можно рассматривать стоянку и процесс паркирования как систему массового обслуживания, где одно место для паркирования является каналом обслуживания, а поступающие на стоянку автомобили будут входящим потоком требований. Число мест для стоянки в такой системе называем числом обслуживающих каналов. С помощью теории массового обслуживания можно количественно оценить качество обслуживания. Качество работы автостоянки показывает, хорошо ли организованно обслуживание, на сколько полно загружены обслуживающие каналы, не велик ли уход из системы необслуженных требовании. Стоянку автомобиля целесообразно считать системой массового обслуживания с потерями. Особенностью функционирования такой системы является то, что всякое требование, поступившее в систему в некоторый момент времени, либо сразу обслуживается, либо теряется, если в момент его поступления все обслуживающие каналы заняты, то есть прибывший на стоянку автомобиль в случае отсутствия свободного места отправляется искать свободную стоянку в другом месте, а исследуемая нами стоянка «несет потери». Оценки функционирования такой системы дает формула А.К. Эрланга, где вероятность того, что обслуживанием заняты k каналов (7),

 , где

 - плотность потока заявок;

n - число мест;

 - параметр обслуживания;

 - среднее время обслуживания требования в системе.

Нехватка каналов обслуживания в стоянках, неравномерная их загрузка порождает еще одну проблему. Значительная часть потоков автомобилей (30-60%) в центральных частях городов высокоавтомобилизированных стран – это ищущие места остановки или стоянки.

Распределение и перераспределение стоящих автомобилей между залами начинается уже на уровне проекта организации движения в масштабе всего города (8).

Эта работа имеет несколько этапов:

1) определение потребностей в стоянках в каждой зоне;

2) определение возможностей стоянки в каждой зоне (наличие мест);

3) определение загрузки стоянки;

4) выработка мер ограничений паркирования автомобилей в разных зонах.

Уровень свободы выбора мест стоянки  зависит от соотношения потребностей  и наличия мест  (7):

1. Анализ существующих способов решения задачи

1.1 Способы решения задачи парковки

В настоящем дипломном проекте рассматривается оптимальное решение задачи парковки, которое основано на статьях зарубежных ученых Renyi, Dvoretzkovo и Robbinsa. Целью их объединенных усилий было создание оптимальной модели паркирования автомобилей на открытой автостоянке. Решением этой задачи парковки автомобилей не являются определенные математические расчеты, которые выражаются в цифрах и количестве расположенных на автостоянке автомобилей относительно выделенной для этого площади. Решением является вывод о законе распределения целочисленной случайной величины -числа машин, занявших место на стоянке при . В словах «оптимальная работа» предусматривается то, что все парковочные места никогда не заняты, но и работает автостоянка не в убыток.

В своей работе Renyi исследовал одномерную задачу о случайном заполнении пространства автостоянки, точнее ряда парковочных мест. Процедура состоит в последовательном расположении автомобилей на отрезке  случайным образом. Интервал  заполняется некоторыми одинаковыми отрезками (автомобилями), условно равными по величине 1 и не имеющими общих точек, то есть не пересекающимися. В итоге решения задачи делается вывод о том, что при достаточно больших  эти отрезки заполняют интервал  на 74,8%. Число отрезков - случайная величина.

Авторы исследуют асимптотическое поведение моментов величины . Доказывается, что величина (нормированная величина ) имеет асимптотически нормальное распределение с параметрами  при .

1.2 Описание предметной области и постановка задачи

Рассмотрим случайный процесс, в котором автомобили длиной «1» паркуются на отрезке  где . Первый автомобиль размещается так, что положение его центра – случайная переменная, имеющая равномерное распределение на отрезке .

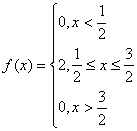 , (a=1)

Если остается пространство для размещения второго автомобиля, то он паркуется так, что его центр – случайная величина, распределенная на отрезке , с расстоянием  от первого автомобиля.

Если на данном отрезке парковки остается пустой промежуток длины , то паркуется третий автомобиль. Его центр – случайная величина, распределенная равномерно, расстояние до разместившихся машин  и так далее до конца отрезка, возможного для парковки.

Обозначим через  число машин, занявших место на стоянке. Тогда  для  и  определено для всех .

Выводы по главе

-задача парковки сводится к исследованию распределения целочисленной случайной величины  при ;

         -итогом решения задачи является то, что при достаточно больших  автомобили заполняют интервал  на 74,8%.

2. Математические методы решения задачи парковки

2.1 Решение задачи парковки

A. Renyi в работе (1) доказал, что математическое ожидание .

 удовлетворяет соотношению  (2.1.1)

где постоянная 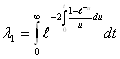 ,  (2.1.2)

В работе (2) соотношение (2.1.1) 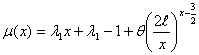 (2.1.3)

и доказано, что среднее квадратическое отклонение

удовлетворяет соотношению  (2.1.4)

где  - некоторая постоянная величина.

Кроме того, доказано, что стандартная случайная величина

имеет предельное нормальное распределение с параметрами от (0,1) при .

Доказывается двумя способами:

а) все моменты сходятся к нормальным моментам при ;

б) непосредственное применение центральной предельной теоремы для сумм независимых случайных величин.

а) нормальное распределение:

плотность вероятности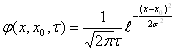

 функция распределения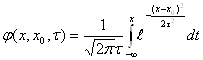

б) центральная предельная теорема:

Если , … - независимо одинаково распределенные случайные величины, и имеющие математическое ожидание  и дисперсию , то при  закон распределения суммы : неограниченно приближается к нормальному (6):

Для решения задачи парковки рассматриваются некоторые интегральные уравнения.

Пусть для  интервал  будет случайным интервалом, занятым первой машиной, вставшей на стоянку на отрезке  длины . Процесс парковки таков, что число машин, которые будут в конце концов размещены от первой, не зависят от числа машин, которые уже размещены на стоянке. При этом число машин, размещенных на отрезке , имеют распределение , а число машин на отрезке  имеют распределение . Следовательно, условное распределение , при условии, что первая машина занимает  такое же, как распределение , где  и  независимы, тогда

 (2.1.5)

Так как  равномерно распределено на , то  (2.1.6)

и для  выполняется интегральное уравнение:

парковка автостоянка математический оптимизация

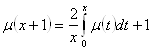,  (2.1.7)

Введем функцию  (2.1.8)

Для  можно записать более простое интегральное уравнение:

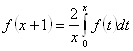
 (2.1.9)

Начальные условия:  при  и  (2.1.10)

тогда можно определить  последовательно на интервалах , ,...

Вычислим  на интервале :

запишем уравнение (2.1.9) в виде: 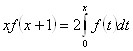 (2.1.11)

Продифференцируем по :  (2.1.12)

сделаем замену: ,

получим:

Рассмотрим решение на интервале  с начальным условием :

 (2.13)

Находим :

тогда

таким образом на интервале .

Аналогично находим  на интервале  с начальными условиями: , , ;

на интервале  с начальными условиями: , , .

Интервал :

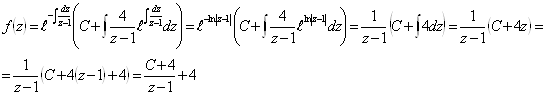
находим , учитывая начальные условия:  при

таким образом  при

Находим

начальные условия на интервале

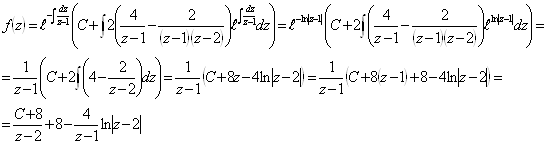
Подставим в решение начальные условия для определения :

таким образом  на интервале .

Дальнейшее интегрирование сложно.

Используя независимость  и  для функции

 (2.1.14)

получаем соотношение  (2.1.15)

Так как , (2.1.16)

то из выражения (2.1.15) следует, что 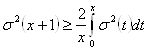 (2.1.17)

Пусть  (2.1.18)

где , найдем для

 (2.1.19)

так как  (2.1.20)

то  (2.1.21)

интегрируя, получим: 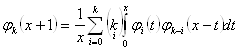 (2.1.22)

2.2 Некоторые сведения из теории вероятности, использованные для решения задачи парковки

Соотношение (2.1.3): 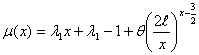 и соотношение (2.1.4):

 получены при использовании теорем.

Теорема 1: пусть  определена для  и удовлетворяет

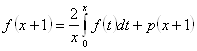 при  (2.2.1) (6)

где  - непрерывна для  и такая, что если  (2.2.2)

,

тогда существует , такая, что полагая

 (2.2.3)

получим

 (2.2.4)

Следствие: если  и  удовлетворяет условию (2.2.1) с

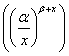 (2.2.5),

то  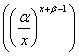(2.2.6)

Теорема 2: пусть  определена для  и удовлетворяет

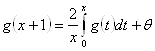
,  где , тогда

 (2.2.7) (6)

Следствие: пусть  определена для  и удовлетворяет

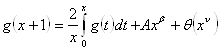
, где  (2.2.8)

тогда  (2.2.9)

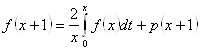
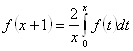Эти теоремы (6) применим к проблеме парковки, так как  удовлетворяет уравнению , (учитываем, что  из (2.1.9)), где ,

(По теореме 1  непрерывна для  и такова, что в предположении , мы имеем , тогда существует  такая, что полагая  имеем

)

то по теореме 1 получается, что:

 (2.2.10)

существует, и что для каждого :

 (2.2.11).

При  из условия ,  получаем, что

 (2.2.12).

Так как  и  приближаются к  очень быстро, то из (2.2.11) получается хорошая аппроксимация.

Так как  для , то грубое приближение  дает

,

следовательно по теореме 1 при условии  следует

Теорема 3: существует постоянная  такая, что математическое ожидание  величины  удовлетворяет соотношению

 () (2.2.13) (6)

Используя формулу Стирлинга , получим

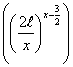 (2.2.14)

Определим и :

, где

Из условия 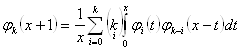, при  получаем

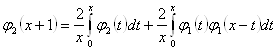, () (2.2.15),

учитывая, что  - левая часть выражения (2.2.14), следовательно

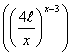 (2.2.15),

таким образом,  удовлетворяет  (),

где оценено формулой (2.2.15).

Из этих условии следует

Теорема 4: существует постоянная  такая, что дисперсия  величины  удовлетворяет соотношению  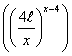(6).

Рассмотрим соотношение:  (2.2.16).

Докажем, что случайная величина  имеет асимптотически нормальное распределение с параметрами  при .

Для доказательства воспользуемся двумя леммами.

Лемма 1: пусть  неотрицательная функция, определенная при , ограниченная на конечных интервалах и удовлетворяющая соотношению , тогда при  выполняется , где  взят по всем наборам неотрицательных , при .

Лемма 2: рассмотрим  такое, что для всех - независимых случайных величин, которые удовлетворяют

 (2.2.17)

следует, что функция распределения  приближается равномерно по  к нормальному распределению с нулевым математическим ожиданием и единичной дисперсией.

Пусть  фиксированная неотрицательная целочисленная функция от, определенная при  и удовлетворяющая условию  и .

Рассмотрим первые  машин, находящихся на отрезке . Обозначим через  расстояние между 0 и самой левой машиной;

- расстояние между этой машиной и машиной, стоящей второй слева и так далее.

- расстояние между машиной, находящейся на правом краю и . Тогда условное распределение , где  такое же, как распределение  при  независимых. Следовательно, условное

распределение  равно распределению , где - независимое и определено

По лемме 1, где  получаем  или

 (2.2.18) для каждого .

Отсюда следует  для условных дисперсии .

Таким образом верно для  для всех достаточно больших  и всех случайных . Из условия  следует .

Пусть - событие:  такое, что , тогда из условия  следует, что  фиксированного  выполняется  и при  удовлетворяет условию .

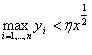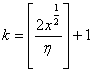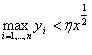Определим функцию , положив  и обозначим  событие: . Возьмем  и разделим отрезок  на  интервалов одинаковой длины, обозначенных , тогда, если условие  неверно, принимается, что, по крайней мере, один из интервалов  разбивается по первым  припаркованным на стоянку машинам.

Вероятность, это меньше, чем 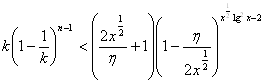 и ,  при  (5). Следовательно, .

Так как  постоянная, выбирая  из выражения  (лемма 2) следует, что  для больших  и тогда  удовлетворяет соотношению  (лемма 2).

Отсюда можно сделать вывод, что условное распределение , данное  есть асимптотически нормальное распределение с параметрами .

Из условия  и  следует, что и само распределение  имеет такое же распределение.

Таким образом доказали, что случайная величина  имеет асимптотически нормальное распределение с параметрами  при  (3).

2.3 Решение интегрального уравнения операционным методом

Применим к решению интегрального уравнения:

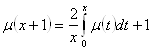,  (2.3.1)

операционный метод Лапласа.

Запишем уравнение в виде: 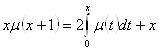, (2.3.2)

продифференцируем его по :

,  (2.3.3)

начальные условия:  при ,

умножим это уравнение на  и обозначим 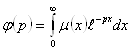, (2.3.4)

где ,

.

Проинтегрируем по  от  до :

 (2.3.5)

Рассмотрим интегралы, входящие в уравнение (3.5):

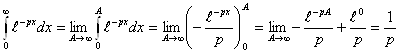 (2.3.6)

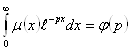 - искомая функция изображения функции  (2.3.7)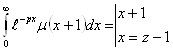

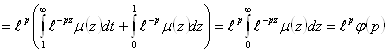 (2.3.8)

 на отрезке  из начальных условий.

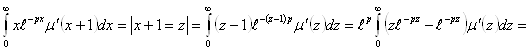
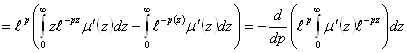
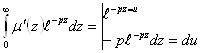
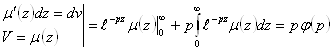
таким образом 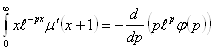 (2.3.9)

Подставляя в уравнение, получим дифференциальное уравнение относительно функции  (4):

 (2.3.10)

Обозначим:

и окончательно  (2.3.11)

Общее решение этого дифференциального уравнения относительно функции  имеет вид (3):

 (2.3.12)

где  - произвольная постоянная, определенная из начальных условии.

Вернемся к исходному уравнению:

 (2.3.13)

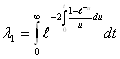где , где  - искомая функция.

Умножим обе части уравнения на  и проинтегрируем по  от  до :

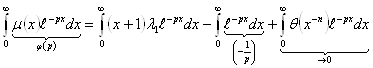
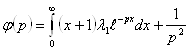 (2.3.14)

из сравнения (3.12) и (3.14) получаем: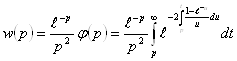

при этом , где 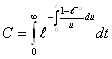 (2.3.15)

 - постоянная величина (вычислена Simon Sandor).

Рассмотрим исходное уравнение: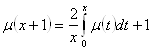

разделим обе части его на  и перейдем к пределу при

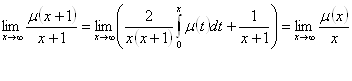
Следовательно, 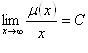, где 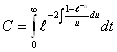 (2.3.16)

из условия  и условия 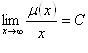 можно получить  (2.3.17)

Так как , то , следовательно, функция  - возрастающая, притом монотонно при .

Умножим исходное уравнение на  и дважды продифференцируем:

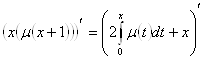
Следовательно,  при  (2.3.18)

Таким образом, искомая кривая  приближается к прямой  при , где .

Итак, можно сделать следующий вывод: если интервал  заполняется некоторыми одинаковыми отрезками, условно равными по величине 1 и не имеющими общих точек (то есть не перекрываются), то при достаточно больших  эти отрезки заполняют интервал  на 74,8%.

Рассмотрим вопрос о вычислении дисперсии.

Пусть в исходном уравнении , тогда  (2.3.19)

(заметим, что ), тогда .

Следовательно, изображение функции  можно записать в виде:

, (2.3.20)

где 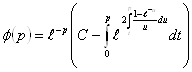. (2.3.21)

Заметим, что функция - целая относительно , и, следовательно,

 - целая функция относительно , тогда функция

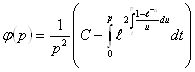 (2.3.22)

тоже целая относительно . Таким образом, для функции  достаточно применить к функции  обратное преобразование Лапласа:

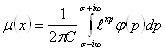
 (2.3.23)

В результате получим:  (2.3.24)

Рассмотрим вопрос о вычислении дисперсии, введя обозначение:

 (2.3.25)

и применим к функции  то же вычисление, как для : на интервале  выбираем интервал , где . Тогда выполняется равенство

, где  и  независимы, так как

,

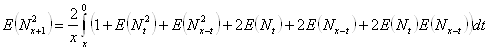то .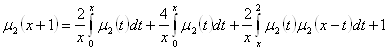

Пусть  (2.3.26)

тогда 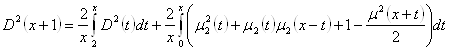 (2.3.27)

Учитывая результаты, полученные для функции  (формула 2.3.24), получаем, что в правой части формулы (2.3.27) функция ограничена, то есть существует некая постоянная величина , что

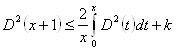 (2.3.28)

Так как функция  удовлетворяет равенству

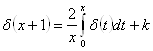 (2.3.29)

то  для любого  и из неравенства (2.3.28) следует,

что , таким образом показано, что

 и  (2.3.30)

Применим неравенство Чебышева для оценки : для любого произвольного положительного числа  выполняется:

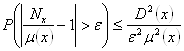 (2.3.31)

Так как , то .

Таким образом получим, что .Можно сделать вывод, что при  достаточно больших, , то есть на интервале отношение закрытой части к полному интервалу очень близко к .

Выводы по главе

- доказано, что случайная величина  имеет асимптотически нормальное распределение с параметрами  при ;

- доказано, что если интервал  заполняется некоторыми одинаковыми отрезками (автомобилями), условно равными по величине 1 и не имеющими общих точек, то при достаточно больших  эти отрезки заполняют интервал  на 74,8%;

- доказано, что при достаточно больших , , то есть на интервале отношение закрытой части к полному интервалу очень близко к .

3. Экономический анализ дипломной работы

3.1 Краткое описание автостоянки

Экономическое обоснование дипломной работы сделаем на конкретном примере новой автостоянки “Стикс”. Автостоянка “Стикс” создана в 2009 году в виде ООО. Генеральным директором компании является Иванов О.Е., которому прин