Скачать

Численные методы анализа

1. Численные методы решения систем линейных уравнений.

1.1 Заданная система

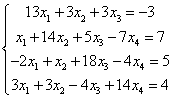
1.2 Метод Гаусса

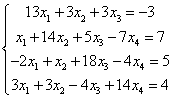   (1.1.)

Прямой ход

Нормируем первое уравнение системы, разделив все члены уравнения на его первый коэффициент при :

         (1.2.)

Умножим нормированное уравнение (1.2) на коэффициенты при х₁ оставшихся уравнений системы (1.1).

(1.3.)

       (1.4.)

                (1.5.)

Вычтем полученные уравнения (1.3.), (1.4.), (1.5.) из второго, третьего и четвёртого уравнения системы (1.1.) соответственно, чтобы исключить из системы х₁:

                 (1.6.)

              (1.7.)

       (1.8.)

Получим новую систему уравнений:

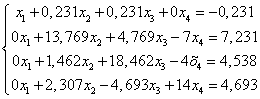    (1.9.)

Рассмотрим систему уравнений (1.9).

Решим систему уравнений без первого уравнения системы (1.9.).

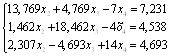    (1.10.)

Нормируем первое уравнение системы (1.10.), разделив все члены уравнения на коэффициент при :

     (1.11.)

Умножаем нормированное уравнение (1.11.) на коэффициент при х₂ оставшихся уравнений:

 (1.12.)

     (1.13.)

Вычтем полученные уравнения (1.12.), (1.13.) из второго и третьего уравнения системы (1.10.) соответственно, чтобы исключить из системы х₂:

                  (1.14.)

          (1.15.)

Получим новую систему уравнений:

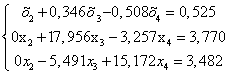           (1.16.)

Рассмотрим систему (1.16) без первого уравнения:

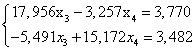         (1.17.)

Нормируем первое уравнение системы (1.17.).

              (1.18.)

Умножаем полученное уравнение (1.18.) на коэффициент при х₄ второго уравнения системы (1.17.):

             (1.19.)

Вычтем полученное уравнение (1.19.) из второго уравнения системы (1.18.):

(1.20.)

Получим новую систему линейных уравнений:

     (1.21.)

Рассмотрим последнее уравнение системы (1.21.).

Нормируем данное уравнение:

           (1.22.)

В результате выполненных действий система (1.1.) приведена к треугольному виду:

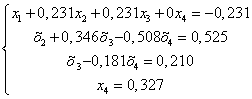       (1.23.)

Обратный ход

x₄ = 0,327;

Найдём  из третьего уравнения системы (1.23.):

x₃ = 0,210+0,181·0,327=0,269;

Найдём  из второго уравнения системы (1.23.):

x₂ = 0,525–0,346·0,269+0,508·0,327 = 0,598;

Найдём  из первого уравнения системы (1.23.):

x₁ = -0,231–0,231·0,598–0,231·0,269+0·0,327 = -0,431

Решением системы линейных уравнений являются значения неизвестных:

Ответ: x₁ = -0,431;

x₂ = 0,598;

x₃ = 0,269;

x₄ = 0,327.

1.3 Метод простой итерации

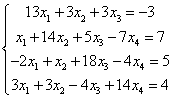
Выполним проверку на сходимость

|a₁₁|>|a₁₂|+|a₁₃|+|a₁₄| → |13|>|3|+|3|+|0|

|a₂₂|>|a₂₁|+|a₂₃|+|a₂₄| → |14|>|1|+|5|+|-7|

|a₃₃|>|a₃₁|+|a₃₂|+|a₃₄| → |18|>|-2|+|1|+|-4|

|a₄₄|>|a₄₁|+|a₄₂|+|a₄₃| → |14|>|3|+|3|+|-4|

Условия сходимости выполняются, следовательно, решение может быть найдено с определенной точностью за некоторое число итераций.

Вычислим значения неизвестных системы линейных алгебраических уравнений с точностью ε  0,001.

Примем за нулевое приближение неизвестных значения, равные нулю, т.е.

x₁⁽⁰⁾ = 0; x₂⁽⁰⁾ = 0; x₃⁽⁰⁾ = 0; x₄⁽⁰⁾ = 0;

Подставим полученные значения в итерационные формулы и вычислим значения неизвестных при первом приближении.

= -0,231

= 0,500

= 0,278

= 0,286

Выполним проверку полученных значений:

|x₁⁽¹⁾-x₁⁽⁰⁾| = |-0,231–0| = 0,231  ε – нет

|x₂⁽¹⁾-x₂⁽⁰⁾| = |0,500–0| = 0,500  ε – нет

|x₃⁽¹⁾-x₃⁽⁰⁾| = |0,278–0| = 0,278  ε – нет

|x₄⁽¹⁾-x₄⁽⁰⁾| = |0,286–0| = 0,286  ε – нет

Выполним вторую итерацию.

Подставим значения неизвестных, полученные в первой итерации, в итерационные формулы и вычислим значения неизвестных при втором приближении.

= -0,410

= 0,560

= 0,288

= 0,308

Выполним проверку полученных значений:

|x₁⁽²⁾-x₁⁽¹⁾| = |-0,410+0,231| = 0,179  ε – нет,

|x₂⁽²⁾-x₂⁽¹⁾| = |0,560–0,500| = 0,060  ε – нет,

|x₃⁽²⁾-x₃⁽¹⁾| = |0,288–0,278| = 0,010  ε – нет,

|x₄⁽²⁾-x₄⁽¹⁾| = |0,308–0,286| = 0,022  ε – нет.

Выполним третью итерацию.

Подставим значения, полученные во втором приближении, в итерационные формулы и вычислим значения неизвестных при третьем приближении.

= -0,427

= 0,580

= 0,270

= 0,336

Выполним проверку полученных значений:

|x₁⁽³⁾-x₁⁽²⁾| = |-0,427+0,410| = 0,017  ε – нет,

|x₂⁽³⁾-x₂⁽²⁾| = |0,580+0,560| = 0,020  ε – нет,

|x₃⁽³⁾-x₃⁽²⁾| = |0,270–0,288| = 0,018  ε – нет,

|x₄⁽³⁾-x₄⁽²⁾| = |0,336–0,308| = 0,028  ε – нет.

Выполним четвёртую итерацию.

Подставим значения, полученные в третьем приближении, в итерационные формулы и вычислим значения неизвестных при четвертом приближении.

= -0,427

= 0,602

= 0,273

= 0,330

Выполним проверку полученных значений:

|x₁⁽⁴⁾-x₁⁽³⁾| = |-0,427+0,427| = 0,000  ε – да,

|x₂⁽⁴⁾-x₂⁽³⁾| = |0,602–0,580| = 0,022  ε – нет,

|x₃⁽⁴⁾-x₃⁽³⁾| = |0,273–0,270| = 0,003  ε – нет,

|x₄⁽⁴⁾-x₄⁽³⁾| = |0,330–0,336| = 0,006  ε – нет.

Выполним пятую итерацию.

Подставим значения, полученные в четвертом приближении, в итерационные формулы и вычислим значения неизвестных при пятом приближении.

= -0,433

= 0,598

= 0,270

= 0,326

Выполним проверку полученных значений:

|x₁⁽⁵⁾-x₁⁽⁴⁾| = |-0,433+0,427| = 0,006  ε – нет,

|x₂⁽⁵⁾-x₂⁽⁴⁾| = |0,598–0,602| = 0,004  ε – нет,

|x₃⁽⁵⁾-x₃⁽⁴⁾| = |0,270–0,273| = 0,003  ε – нет,

|x₄⁽⁵⁾-x₄⁽⁴⁾| = |0,326–0,330| = 0,004  ε – нет.

Выполним шестую итерацию.

Подставим значения, полученные в пятом приближении, в итерационные формулы и вычислим значения неизвестных при шестом приближении.

= -0,431

= 0,597

= 0,269

= 0,327

Выполним проверку полученных значений:

|x₁⁽⁶⁾-x₁⁽⁵⁾| = |-0,431+0,433| = 0,002  ε – нет,

|x₂⁽⁶⁾-x₂⁽⁵⁾| = |0,597–0,598| = 0,001  ε – да,

|x₃⁽⁶⁾-x₃⁽⁵⁾| = |0,269–0,270| = 0,001  ε – да,

|x₄⁽⁶⁾-x₄⁽⁵⁾| = |0,327–0,326| = 0,001  ε – да.

Выполним седьмую итерацию.

Подставим значения, полученные в шестом приближении, в итерационные формулы и вычислим значения неизвестных при седьмом приближении.

= -0,431

= 0,598

= 0,269

= 0,327

Выполним проверку полученных значений:

|x₁⁽⁷⁾-x₁⁽⁶⁾| = |-0,431+0,431| = 0,000  ε – да,

|x₂⁽⁷⁾-x₂⁽⁶⁾| = |0,598–0,597| = 0,001  ε – да,

|x₃⁽⁷⁾-x₃⁽⁶⁾| = |0,269–0,269| = 0,000  ε – да,

|x₄⁽⁷⁾-x₄⁽⁶⁾| = |0,327–0,327| = 0,000  ε – да.

Необходимая точность достигается в седьмой итерации.

Ответ:       х₁ = -0,431,

х₂ = 0,598,

х₃ = 0,269,

х₄ = 0,327.

1.4 Метод Зейделя

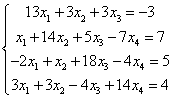
Условия сходимости было проверено выше, оно выполняется.

Точность вычисления ε  0,001.

Примем за нулевое приближение неизвестных значений, равные нулю.

x₁⁽⁰⁾ = x₂⁽⁰⁾ = x₃⁽⁰⁾ = x₄⁽⁰⁾ = 0;

Подставим полученные значения в итерационные формулы и вычислим значения неизвестных при первом приближении.

= -0,231

= 0,517

= 0,223

= 0,288

Выполним проверку полученных значений:

|x₁⁽¹⁾-x₁⁽⁰⁾| = |-0,231–0| = 0,231  ε – нет

|x₂⁽¹⁾-x₂⁽⁰⁾| = |0,517–0| = 0,517  ε – нет

|x₃⁽¹⁾-x₃⁽⁰⁾| = |0,223–0| = 0,223  ε – нет

|x₄⁽¹⁾-x₄⁽⁰⁾| = |0,288–0| = 0,288  ε – нет

Выполним вторую итерацию.

Подставим значения, полученные в первом приближении, в итерационные формулы и вычислим значения неизвестных при втором приближении.

= -0,402

= 0,593

= 0,264

= 0,320

Выполним проверку полученных значений:

|x₁⁽²⁾-x₁⁽¹⁾| = |-0,402+0,231| = 0,171  ε – нет,

|x₂⁽²⁾-x₂⁽¹⁾| = |0,593–0,517| = 0,076  ε – нет,

|x₃⁽²⁾-x₃⁽¹⁾| = |0,264–0,223| = 0,041  ε – нет,

|x₄⁽²⁾-x₄⁽¹⁾| = |0,320–0,288| = 0,032  ε – нет.

Выполним третью итерацию.

Подставим значения, полученные во втором приближении, в итерационные формулы и вычислим значения неизвестных при третьем приближении.

= -0,429

= 0,596

= 0,268

= 0,326

Выполним проверку полученных значений:

|x₁⁽³⁾-x₁⁽²⁾| = |-0,429+0,402| = 0,027  ε – нет,

|x₂⁽³⁾-x₂⁽²⁾| = |0,596–0,593| = 0,003  ε – нет,

|x₃⁽³⁾-x₃⁽²⁾| = |0,268–0,264| = 0,004  ε – нет,

|x₄⁽³⁾-x₄⁽²⁾| = |0,326–0,320| = 0,006  ε – нет.

Выполним четвёртую итерацию.

Подставим значения, полученные в третьем приближении, в итерационные формулы и вычислим значения неизвестных при четвёртом приближении.

= -0,430

= 0,598

= 0,269

= 0,327

Выполним проверку полученных значений:

|x₁⁽⁴⁾-x₁⁽³⁾| = |-0,430+0,429| = 0,01  ε – да,

|x₂⁽⁴⁾-x₂⁽³⁾| = |0,598–0,596| = 0,002  ε – нет,

|x₃⁽⁴⁾-x₃⁽³⁾| = |0,269–0,268| = 0,001  ε – да,

|x₄⁽⁴⁾-x₄⁽³⁾| = |0,327–0,326| = 0,001  ε – да.

Выполним пятую итерацию.

Подставим значения, полученные в четвёртом приближении, в итерационные формулы и вычислим значения неизвестных при пятом приближении.

= -0,431

= 0,598

= 0,269

= 0,327

Выполним проверку полученных значений:

|x₁⁽⁵⁾-x₁⁽⁴⁾| = |-0,431+0,430| = 0,001  ε – да,

|x₂⁽⁵⁾-x₂⁽⁴⁾| = |0,598–0,598| = 0,000  ε – да,

|x₃⁽⁵⁾-x₃⁽⁴⁾| = |0,269–0,269| = 0,000  ε – да,

|x₄⁽⁵⁾-x₄⁽⁴⁾| = |0,327–0,327| = 0,000  ε – да.

Необходимая точность достигается в пятой итерации.

Ответ:       х₁ = -0,431,

х₂ = 0,598,

х₃ = 0,269,

х₄ = 0,327.

2. Численные методы аппроксимации и интерполяции функций

2.1 Задание

Найти интерполяционный полином второго порядка

методом неопределённых коэффициентов, используя данные нулевого, второго и четвёртого опытов.

Найти аппроксимирующий полином первого порядка

методом наименьших квадратов.

Исходные данные

                   0                 1                 2                          3                 4