Потрійний інтеграл
ПОТРІЙНИЙ ІНТЕГРАЛ
1. Поняття потрійного інтеграла. Умови його існування та властивості
Схема побудови потрійного інтеграла така сама, як і звичайного визначеного інтеграла та подвійного інтеграла.
Нехай функція ![]() визначена в обмеженій замкненій області
визначена в обмеженій замкненій області ![]() . Розіб'ємо область
. Розіб'ємо область ![]() сіткою поверхонь на
сіткою поверхонь на ![]() частин
частин ![]() , які не мають спільних внутрішніх точок і об'єми яких дорівнюють
, які не мають спільних внутрішніх точок і об'єми яких дорівнюють ![]() . У кожній частині
. У кожній частині ![]() візьмемо довільну точку
візьмемо довільну точку ![]() і утворимо суму
і утворимо суму
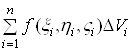 ,(1)
,(1)
яка називається інтегральною сумою для функції ![]() за областю
за областю ![]() . Нехай
. Нехай ![]() – найбільший з діаметрів областей
– найбільший з діаметрів областей ![]() .
.
Якщо інтегральна сума (1) при ![]() має скінченну границю, яка не залежить ні від способу розбиття області
має скінченну границю, яка не залежить ні від способу розбиття області ![]() на частини
на частини ![]() , ні від вибору в них точок
, ні від вибору в них точок ![]() , то ця границя називається потрійним інтегралом і позначається одним із таких символів:
, то ця границя називається потрійним інтегралом і позначається одним із таких символів:
![]() або
або ![]() .
.
Таким чином, за означенням
 ,(2)
,(2)
де ![]() – функція, інтегровна в області
– функція, інтегровна в області ![]() ;
; ![]() – область інтегрування;
– область інтегрування; ![]() і
і ![]() – змінні інтегрування;
– змінні інтегрування; ![]() (або
(або ![]() ) – елемент об'єму.
) – елемент об'єму.
Якщо по тілу ![]() розподілено масу з об'ємною густиною
розподілено масу з об'ємною густиною ![]() в точці
в точці ![]() , то маса
, то маса ![]() цього тіла знаходиться за формулою
цього тіла знаходиться за формулою
![]() . (3)
. (3)
Формула (3) аналогічна формулі (1.8) і може розглядатися як механічний зміст потрійного інтеграла, коли підінтегральна функція невід'ємна в області ![]() . Якщо всюди в області покласти
. Якщо всюди в області покласти ![]() , то з формули (2) випливає формула для обчислення об'єму
, то з формули (2) випливає формула для обчислення об'єму ![]() тіла
тіла ![]() :
:
![]() .(4)
.(4)
Потрійний інтеграл є безпосереднім узагальненням подвійного інтеграла на тривимірний простір. Теорія потрійного інтеграла аналогічна теорії подвійного інтеграла, тому в більшості випадків ми обмежимося лише формулюваннями тверджень і короткими поясненнями.
Теорема (достатня умова інтегровності функції). Якщо функція ![]() неперервна в обмеженій замкненій області
неперервна в обмеженій замкненій області ![]() , то вона в цій області інтегрована.
, то вона в цій області інтегрована.
Властивості потрійних інтегралів.
1. Сталий множник можна винести за знак потрійного інтеграла:
![]() .
.
Потрійний інтеграл від суми кількох інтегровних функцій дорівнює сумі потрійних інтегралів від доданків:
![]() .
.
3. Якщо в області інтегрування ![]() , то
, то
![]() .
.
4. Якщо функції ![]() та
та ![]() визначені в одній і тій самій області
визначені в одній і тій самій області ![]() і
і ![]() , то
, то
![]() .
.
5. (Адитивність потрійного інтеграла.) Якщо область інтегрування ![]() функції
функції ![]() розбити на частини
розбити на частини ![]() і
і ![]() , які не мають спільних внутрішніх точок, то
, які не мають спільних внутрішніх точок, то
![]() .
.
6. (Оцінка потрійного інтеграла.) Якщо функція ![]() неперервна в обмеженій замкненій області
неперервна в обмеженій замкненій області ![]() , яка має об'єм
, яка має об'єм ![]() , то
, то
![]() ,
,
де ![]() і
і ![]() відповідно найменше і найбільше значення функції
відповідно найменше і найбільше значення функції ![]() в області
в області ![]() .
.
7. (Середнє значення функції.) Якщо функція ![]() неперервна в обмеженій замкненій області
неперервна в обмеженій замкненій області ![]() , яка має об'єм
, яка має об'єм ![]() , то в цій області існує така точка
, то в цій області існує така точка ![]() , що
, що
![]() .
.
Величина
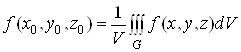
називається середнім значенням функції ![]() в області
в області ![]() .
.
2. Обчислення потрійного інтеграла
Обчислення потрійного інтеграла зводять до обчислення повторних, тобто до інтегрування за кожною змінній окремо.
Нехай область ![]() обмежена знизу і зверху поверхнями
обмежена знизу і зверху поверхнями ![]() і
і ![]() , а з боків циліндричною поверхнею, твірні якої паралельні осі
, а з боків циліндричною поверхнею, твірні якої паралельні осі ![]() . Позначимо проекцію області
. Позначимо проекцію області ![]() на площину
на площину ![]() через
через ![]() (рис. 1) і вважатимемо, що функції
(рис. 1) і вважатимемо, що функції ![]() і
і ![]() неперервні в
неперервні в ![]() .
.
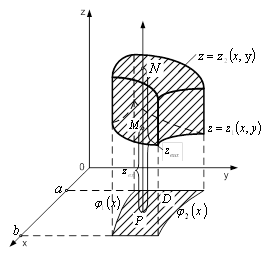
Рисунок 1 – Область ![]()
Якщо при цьому область ![]() є правильною, то область
є правильною, то область ![]() називається правильною у напрямі осі
називається правильною у напрямі осі ![]() . Припустимо, що кожна пряма, яка проходить через кожну внутрішню точку
. Припустимо, що кожна пряма, яка проходить через кожну внутрішню точку ![]() паралельно осі
паралельно осі ![]() , перетинає межу області
, перетинає межу області ![]() у точках
у точках ![]() і
і ![]() . Точку
. Точку ![]() назвемо точкою входу в область
назвемо точкою входу в область ![]()
![]() , а точку
, а точку ![]() – точкою виходу з області
– точкою виходу з області ![]() , а їхні аплікати позначимо відповідно через
, а їхні аплікати позначимо відповідно через ![]() і
і ![]() . Тоді
. Тоді ![]() ,
, ![]() і для будь-якої неперервної в області
і для будь-якої неперервної в області ![]() функції
функції ![]() має місце формула
має місце формула
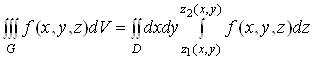 .(5)
.(5)
Зміст формули (5) такий. Щоб обчислити потрійний інтеграл, потрібно спочатку обчислити інтеграл 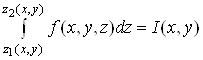 за змінною
за змінною ![]() , вважаючи
, вважаючи ![]() та
та ![]() сталими. Нижньою межею цього інтеграла є апліката точки
сталими. Нижньою межею цього інтеграла є апліката точки ![]() входу
входу ![]() , а верхньою – апліката
, а верхньою – апліката ![]() точки виходу
точки виходу ![]() . Внаслідок інтегрування отримаємо функцію
. Внаслідок інтегрування отримаємо функцію ![]() від змінних
від змінних ![]() та
та ![]() .
.
Якщо область ![]() , наприклад, обмежена кривими
, наприклад, обмежена кривими ![]() і
і ![]()
![]() , де
, де ![]() і
і ![]() – неперервні функції, тобто
– неперервні функції, тобто
![]() , то, переходячи від подвійного інтеграла
, то, переходячи від подвійного інтеграла ![]() до повторного (п. 1.3), отримаємо формулу
до повторного (п. 1.3), отримаємо формулу
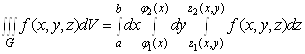 ,(6)
,(6)
яка зводить обчислення потрійного інтеграла до послідовного обчислення трьох визначених інтегралів. Порядок інтегрування може бути й іншим, тобто змінні ![]() і
і ![]() у правій частині формули (6) за певних умов можна міняти місцями.
у правій частині формули (6) за певних умов можна міняти місцями.
Якщо, наприклад, область ![]() правильна в напрямі осі
правильна в напрямі осі ![]() :
:
![]() ,
,
де ![]() – неперервні функції, то
– неперервні функції, то
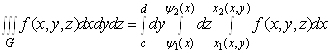 .
.
Зокрема, якщо областю інтегрування є паралелепіпед:
![]() ,
,
то
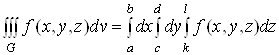 . (7)
. (7)
У цьому разі інтегрування виконується в будь-якому порядку, оскільки область ![]() правильна у напрямі всіх трьох координатних осей
правильна у напрямі всіх трьох координатних осей ![]() .
.
3. Заміна змінних в потрійному інтегралі
Заміну змінної в потрійному інтегралі виконують за таким правилом: якщо обмежена замкнена область ![]() взаємно однозначно відображується на область
взаємно однозначно відображується на область ![]() за допомогою неперервно диференційовних функцій
за допомогою неперервно диференційовних функцій ![]() ,
, ![]() ,
, ![]() , якобіан
, якобіан ![]() в області
в області ![]() не дорівнює нулю:
не дорівнює нулю:

і ![]() – неперервна в
– неперервна в ![]() , то справедлива формула
, то справедлива формула
![]() . (8)
. (8)
На практиці найуживанішими є циліндричні та сферичні координати. При переході від прямокутних координат ![]() до циліндричних
до циліндричних ![]() (рис.4, а), пов'язаних з
(рис.4, а), пов'язаних з ![]() співвідношеннями
співвідношеннями
![]() ;
;
![]() ,
,
якобіан перетворення
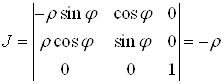 .
.
З формули (8) отримуємо потрійний інтеграл у циліндричних координатах:
![]() .(9)
.(9)
Назва «циліндричні координати» пов'язана з тим, що координатна поверхня ![]() є циліндром, прямолінійні твірні якого паралельні осі
є циліндром, прямолінійні твірні якого паралельні осі ![]() .
.
При переході від прямокутних координат ![]() до сферичних
до сферичних ![]()
(рис. 4, б), які пов'язані з ![]() формулами
формулами
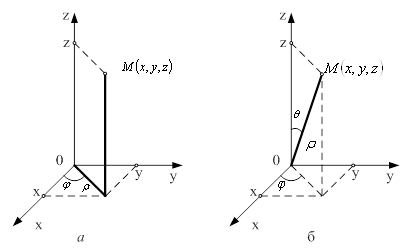
Рисунок 4 – Координати: а) циліндричні; б) сферичні
![]() ;
;
![]() ,
,
якобіан перетворення
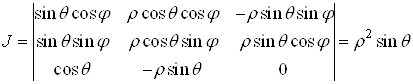 .
.
З формули (8) знаходимо потрійний інтеграл у сферичних координатах:
![]() . (10)
. (10)
Назва «сферичні координати» пов'язана з тим, що координатна поверхня ![]() є сферою. При обчисленні потрійного інтеграла в циліндричних чи сферичних координатах область
є сферою. При обчисленні потрійного інтеграла в циліндричних чи сферичних координатах область ![]() , як правило, не будують, а межі інтегрування знаходять безпосередньо за областю
, як правило, не будують, а межі інтегрування знаходять безпосередньо за областю ![]() , користуючись геометричним змістом нових координат. При цьому рівняння поверхонь
, користуючись геометричним змістом нових координат. При цьому рівняння поверхонь ![]() та
та ![]() , які обмежують область
, які обмежують область ![]() , записують у нових координатах.
, записують у нових координатах.
Зокрема, якщо область ![]() обмежена циліндричною поверхнею
обмежена циліндричною поверхнею ![]() та площинами
та площинами ![]() , то всі межі інтегрування в циліндричній системі координат сталі:
, то всі межі інтегрування в циліндричній системі координат сталі:
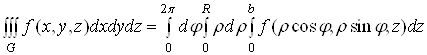
і не змінюються при зміні порядку інтегрування. Те саме буде у сферичних координатах у випадку, коли ![]() – куля:
– куля: ![]() або кульове кільце. Наприклад, якщо
або кульове кільце. Наприклад, якщо ![]() – кульове кільце з внутрішньою сферою
– кульове кільце з внутрішньою сферою ![]() , то рівняння цієї сфери в сферичних координатах має вигляд
, то рівняння цієї сфери в сферичних координатах має вигляд
![]()
або
![]() ,
,
звідки ![]() . Аналогічно
. Аналогічно ![]() – рівняння зовнішньої сфери, тому
– рівняння зовнішньої сфери, тому
![]() .
.
У випадку, коли ![]() – куля
– куля ![]() , у цій формулі слід покласти
, у цій формулі слід покласти ![]() . Інших будь-яких загальних рекомендацій, коли необхідно переходити до тієї чи іншої системи координат, дати неможливо. Це залежить і від області інтегрування, і від підінтегральної функції. Іноді потрібно написати інтеграл у різних системах координат і лише після цього вирішити, в якій з них обчислення буде найпростішим.
. Інших будь-яких загальних рекомендацій, коли необхідно переходити до тієї чи іншої системи координат, дати неможливо. Це залежить і від області інтегрування, і від підінтегральної функції. Іноді потрібно написати інтеграл у різних системах координат і лише після цього вирішити, в якій з них обчислення буде найпростішим.
Приклад
1. Обчислити інтеграл ![]() , якщо область
, якщо область ![]() обмежена поверхнями
обмежена поверхнями ![]() і
і ![]() .
.
Розв’язання
Область ![]() є конусом (рис. 5).
є конусом (рис. 5).
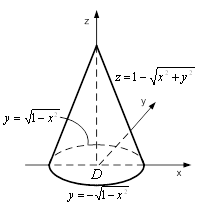
Рисунок 5 – Область ![]()
Рівняння конічної поверхні, яка обмежує область ![]() , можна записати у вигляді
, можна записати у вигляді ![]() , а саму область
, а саму область ![]() подати таким чином:
подати таким чином: ![]() , де
, де ![]() – круг радіуса
– круг радіуса ![]() з центром
з центром ![]() . Тому даний потрійний інтеграл можна звести до послідовного обчислення трьох визначених інтегралів у прямокутних координатах:
. Тому даний потрійний інтеграл можна звести до послідовного обчислення трьох визначених інтегралів у прямокутних координатах:
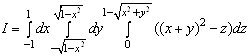 .
.
Проте зручніше перейти до циліндричних координат ![]() . Тоді прообраз круга
. Тоді прообраз круга ![]() є прямокутник
є прямокутник ![]() , прообраз конічної поверхні – плоска поверхня
, прообраз конічної поверхні – плоска поверхня ![]() , а прообраз області
, а прообраз області ![]() – область
– область ![]() . Якобіан переходу до циліндричних координат дорівнює
. Якобіан переходу до циліндричних координат дорівнює ![]() , підінтегральна функція в циліндричних координатах дорівнює
, підінтегральна функція в циліндричних координатах дорівнює![]() . Зводячи потрійний інтеграл за областю
. Зводячи потрійний інтеграл за областю ![]() до послідовного обчислення трьох визначних інтегралів, отримаємо
до послідовного обчислення трьох визначних інтегралів, отримаємо
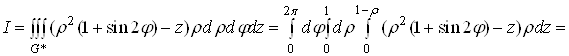
![]()
Зазначимо, що розставлення меж інтегрування в циліндричних координатах, як правило, виконують, розглядаючи не область ![]() , а зміну циліндричних координат в області
, а зміну циліндричних координат в області ![]() . Наочно видно, що в області
. Наочно видно, що в області ![]() змінна
змінна ![]() змінюється від
змінюється від ![]() до
до ![]() , при кожному значенні
, при кожному значенні ![]() змінна
змінна ![]() змінюється від
змінюється від ![]() до
до ![]() , а для кожної точки
, а для кожної точки ![]() області
області ![]() змінна
змінна ![]() змінюється в області
змінюється в області ![]() від
від ![]() (значення
(значення ![]() в області
в області ![]() ) до
) до ![]() (значення
(значення ![]() на конічній поверхні).
на конічній поверхні).
4. Деякі застосування потрійного інтеграла
інтеграл потрійний обчислення змінний
1. Обчислення об'ємів. Якщо деяке тіло є обмеженою і замкненою
областю ![]() , що має об'єм
, що має об'єм ![]() , то згідно з формулою (4)
, то згідно з формулою (4)
![]() .(11)
.(11)
Застосування у механіці. Нехай ![]() – обмежена замкнена область простору
– обмежена замкнена область простору ![]() , яку займає деяке матеріальне тіло з густиною
, яку займає деяке матеріальне тіло з густиною ![]() , де
, де ![]() – неперервна функція в області
– неперервна функція в області ![]() , тоді:
, тоді:
а)маса цього тіла
![]() ;(12)
;(12)
б)моменти інерції ![]() тіла відносно координатних осей
тіла відносно координатних осей ![]() відповідно дорівнюють
відповідно дорівнюють
![]() . (13)
. (13)
Моменти інерції ![]() тіла відносно координатних площин
тіла відносно координатних площин ![]() обчислюються за формулами
обчислюються за формулами
![]() .(14)
.(14)
Момент інерції тіла відносно початку координат
![]()
![]() (15)
(15)
в) статичні моменти ![]() тіла відносно координатних площин
тіла відносно координатних площин ![]() обчислюються за формулами
обчислюються за формулами
![]() ;(16)
;(16)
г) координати ![]() центра маси тіла визначаються за формулами
центра маси тіла визначаються за формулами
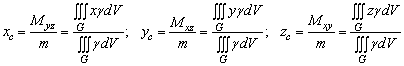 . (17)
. (17)
Доведення формули (11), як уже зазначалося, випливає з означення потрійного інтеграла:
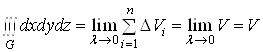 .
.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Системи лінійних рівнянь
- Алгоритмічні проблеми
- Дослідження лінійно впорядкованого простору ординальних чисел
Курсова робота: Дослідження лінійно впорядкованого простору ординальних чиселЗмістВведенняРозділ 1.Вихідні визначення§1. Порядкові в
- Дослідження топологічного визначення верхніх напівґрат
- Застосування подвійних інтегралів
- Интегралы, зависящие от параметра
Математический анализ - общеобразовательная математическая дисциплина, объектом изучения которой является большая часть математики,
- Интеграционный метод Эйлера для решения линейных систем алгебраических уравнений
 www.referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
www.referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

