www.referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
Математическая модель в пространстве состояний линейного стационарного объекта управления
СОДЕРЖАНИЕ
1. Анализ объекта управления
1.1 Анализ линейного стационарного объекта управления, заданного передаточной функцией
1.2 Получение математической модели в пространстве состояний линейного стационарного объекта управления, заданного передаточной функцией
1.2.1 Матрица Фробениуса
1.2.2 Метод параллельной декомпозиции
2. Решение задачи быстродействия симплекс-методом
3. Оптимальная l – проблема моментов
3.1 Оптимальная l – проблема моментов в пространстве «вход-выход»
3.2 Оптимальная l – проблема моментов в пространстве состояний
4. Нахождение оптимального управления с использованием грамиана управляемости (критерий – минимизация энергии)
5. Аналитическое конструирование оптимальных регуляторов (акор)
5.1 Стабилизации объекта управления на полубесконечном интервале времени
5.1.1 Решение алгебраического уравнения Риккати методом диагонализации
5.1.2 Решение алгебраического уравнения Риккати интегрированием в обратном времени до установившегося состояния
5.2 Стабилизации объекта управления на конечном интервале времени
5.3 Задача акор – стабилизации для компенсации известного возмущающего воздействия.
5.4 Задача акор для отслеживания известного задающего воздействия. i подход
5.5 Задача акор для отслеживания известного задающего воздействия. ii подход (линейный сервомеханизм)
5.6 Задача акор – слежения со скользящими интервалами.
6. Синтез наблюдателя полного порядка
Литература
Приложение
PlotTimeFrHaract.m
ProstranstvoSostoyanii.m
SimplexMetod2.m
Optimal_L_problem_moments.m
Gramian_Uprav.m
AKOR_stabilizaciya_na_polybeskon_interval.m
AKOR_stabilizaciya_na_konech_interval.m
Sravnenie_stabilizacii.m
AKOR_stabilizaciya_pri_vozmusheniyah.m
AKOR_slegenie_na_konech_interval_I_podxod.m
AKOR_slegenie_na_konech_interval_II_podxod.m
AKOR_slegenie_so_skolz_intervalami_Modern.m
Sintez_nablyud_polnogo_poryadka.m
Solve_Riccati_Method_Diag.m
Solve_Riccati_Method_Revers_Integr.m
Vozmyshyayushee_Vozdeistvie_Discrete_Revers.m
Zadayushee_Vozdeistvie_Discrete_Revers_Modern.m
1.1 Анализ линейного стационарного объекта управления, заданного передаточной функцией
Передаточная функция данного объекта имеет вид:
,
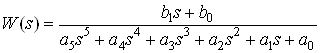где:
, 
;
, 
, 
, 
, 
, 
.
или
.
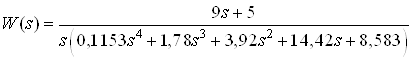Нули передаточной функции:
Полюса передаточной функции (полученные стандартными функциями среды Matlab 7.4):
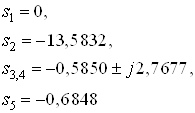
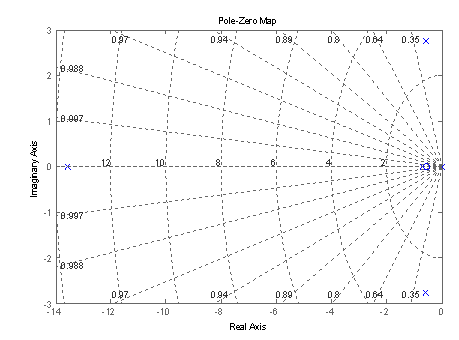
Рис.1. График расположения нулей и полюсов передаточной функции объекта на комплексной плоскости.
Найдем временные характеристики объекта управления.
К временным характеристикам относятся 
и
.
– переходная характеристика;
– импульсная переходная функция;
Для нахождения и воспользуемся пакетом Matlab 7.4.
,
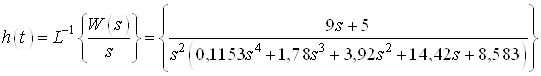Аналитическое выражение для :
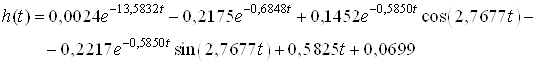
В этом случае имеет вид
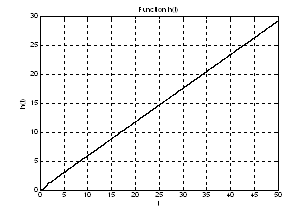
Рис.2. График переходной характеристики .
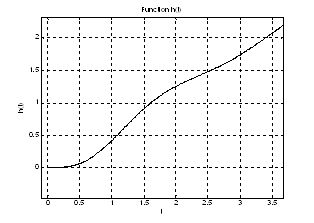
Рис.3. График переходной характеристики на интервале 
(увеличенное).
,
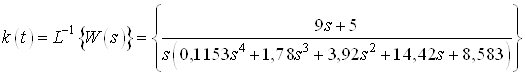Аналитическое выражение для :
.
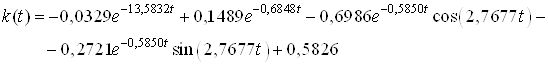В этом случае имеет вид
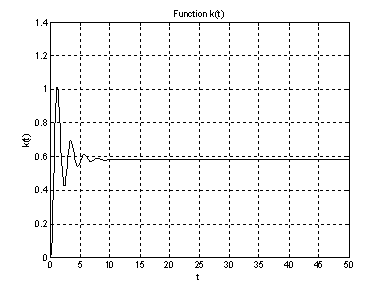
Рис.4. График импульсной переходной характеристики .
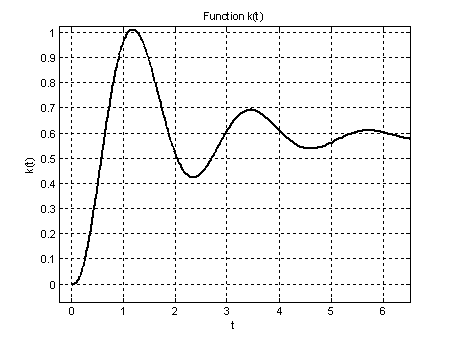
Рис.5. График импульсной переходной характеристики на интервале 
(увеличенное).
Найдем частотные характеристики объекта управления.
К частотным характеристикам относятся:
амплитудно – частотная характеристика (АЧХ),
фазо – частотная характеристика (ФЧХ),
амплитудно – фазовая частотная характеристика (АФЧХ),
Аналитическое выражение для АЧХ:
.
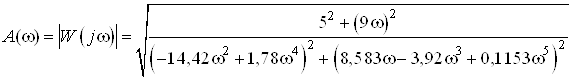В этом случае АЧХимеет вид
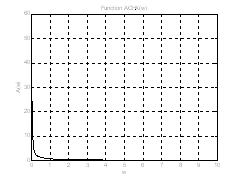
Рис.6. График АЧХ
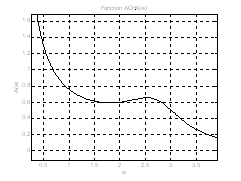
Рис.7. График АЧХ на интервале 
(увеличенное). Аналитическое выражение для ФЧХ:
В этом случае ФЧХимеет вид
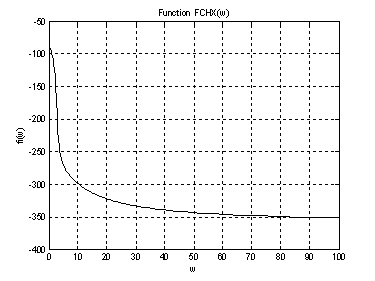
Рис.8. График ФЧХ .
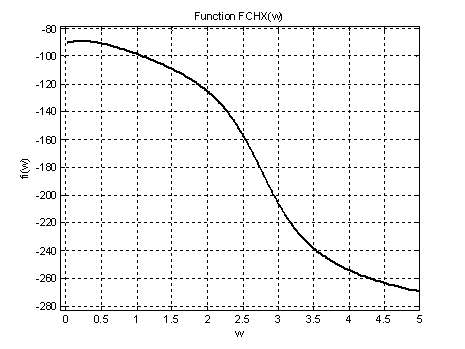
Рис.9. График ФЧХ на интервале 
(увеличенное).
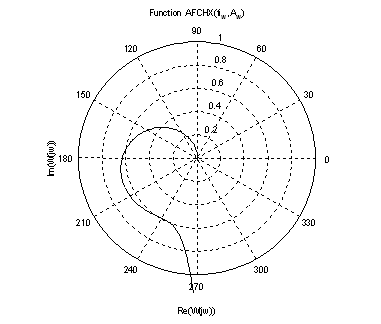
Рис.10. График АФЧХ.
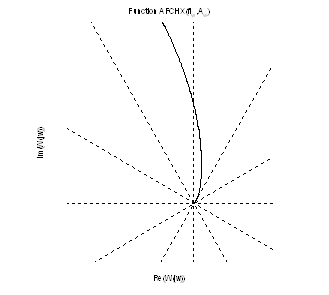
Рис.11. График АФЧХ (увеличенное).
Аналитическое выражение для ЛАЧХ:
.
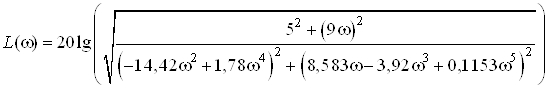В этом случае ЛАЧХ имеет вид
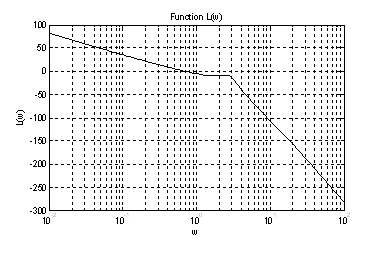
Рис.12. График ЛАЧХ.
Аналитическое выражение для ЛФЧХ:
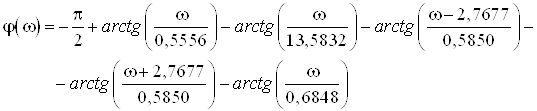
В этом случае ЛФЧХ имеет вид
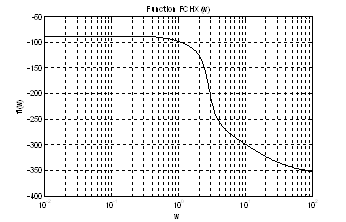
Рис.13. График ЛФЧХ.
1.2 Получение математической модели в пространстве состояний линейного стационарного объекта управления, заданного передаточной функцией
Передаточная функция данного объекта имеет вид:
,
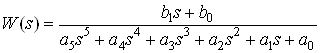где:
, ;
, , , , , .
или
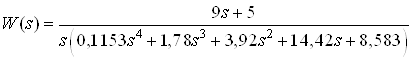
Описание системы в пространстве состояний имеет следующий вид:
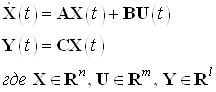
Переходя в область изображений описание системы в пространстве состояний будет иметь следующий вид:
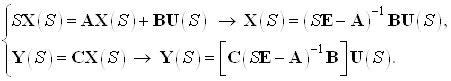
1.2.1 Матрица Фробениуса
Получим выражения, которые определяют вектор состояний и выход заданного объекта в общем виде:
.
.
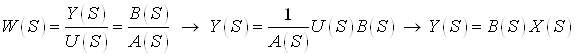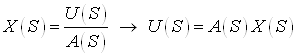Тогда получим:
(1)
(2)
Числитель передаточной функции имеет вид: 
.
Знаменатель передаточной функции:
.
Тогда согласно равенству (1) и (2) имеем
,
.
Перейдем из области изображений в область оригиналов
,
и затем перейдем к нормальной форме Коши
.
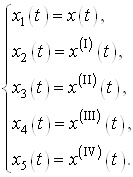
Запишем матрицы состояний
, 
, 
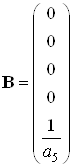Численное значение матриц состояний:
, 
,
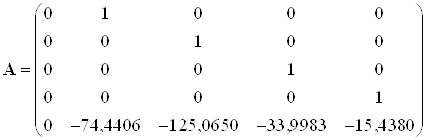1.2.2 Метод параллельной декомпозиции
Запишем передаточную функцию объекта в другом виде, а именно:
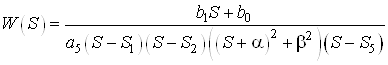
или
.
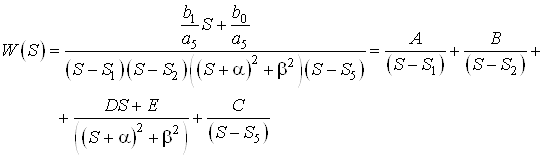Согласно формуле 
получим
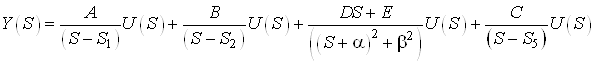
Рассмотрим каждое из слагаемых в отдельности согласно принципу параллельной декомпозиции.
a.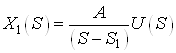 
,
.
b.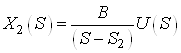 
,
.
c.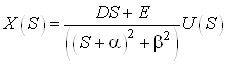 
,
,
,
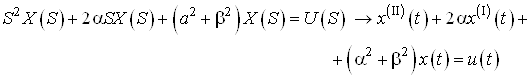
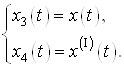
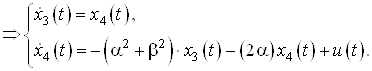
d.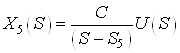 
,
Получим выход системы:
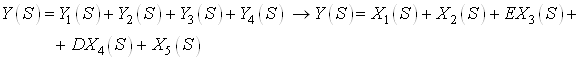
Запишем матрицы состояний
, 
, 
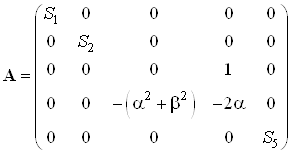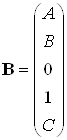Вычисление коэффициентов разложения дробной рациональной функции 
на сумму элементарных дробей и проверка правильности получения матриц состояния сделано с помощью пакета Matlab 7.4 (скрипт ProstranstvoSostoyanii.m)
Получены следующие результаты:Матрица СЛАУ:
, 
,
,
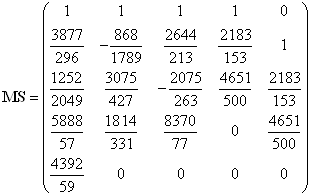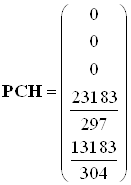
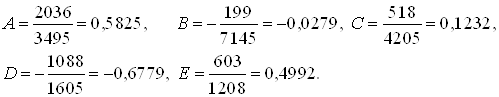
Численное значение матриц состояний:
, 
,
.
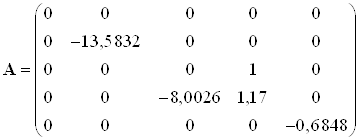2. Решение задачи быстродействия симплекс-методом
Дана система:
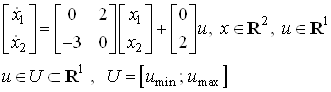(3)
1. Проверим управляемость данной системы.
Запишем систему ДУ в матричном виде:
,
где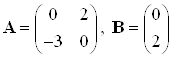 
.
Данная система является стационарной, её порядок 
, поэтому матрица управляемости имеет вид:
Найдем матрицу управляемости:
Ранг матрицы управляемости равен порядку системы, следовательно, данная система является управляемой.
следовательно 
.
Собственные числа матрицы 
найдем из уравнения 
:
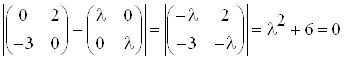
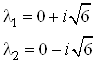
Действительные части собственных значений матрицы являются неположительными, следовательно, все условия управляемости выполнены.
2. Ссылаясь на решение задачи быстродействия из ДЗ№2 по СУЛА «Решение задачи быстродействия» имеем:
Запишем зависимости 
, 
, полученные при решении систем дифференциальных уравнений:
:
:
:
:
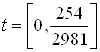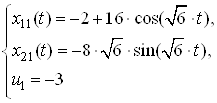
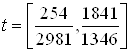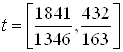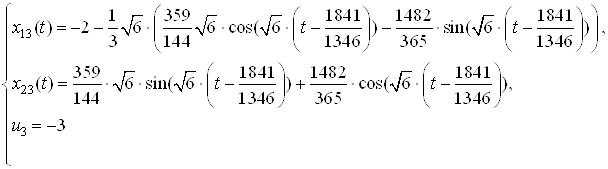
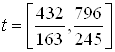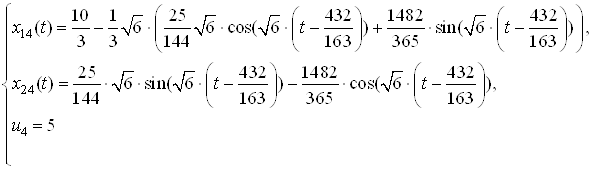
Перейдем к дискретной модели заданной системы. Имеем
(4)
где 
шаг дискретизации и соответствующие матрицы
(5)
Пусть управление ограничено интервальным ограничением
(6)
Тогда на 
шаге имеем
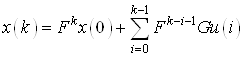(7)
Известны начальная и конечная точки
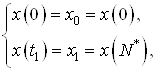
где 
– оптимальное число шагов в задаче быстродействия.
Решается задача быстродействия
а) Формирование задачи быстродействия как задачи линейного программирования
Конечная точка 
в дискретной модели представлена в виде
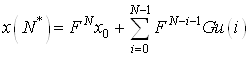(8)
Получаем 
– равенств
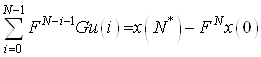(9)
Для приведения ограничений (9) к канонической форме сделаем необходимое преобразование в правой и левой частях, чтобы правые части были неотрицательными (если правая часть меньше нуля, то домножаем на (-1) левую и правую части). Отметим проведенные измененияточкой в правом верхнем углу соответствующих векторов
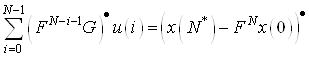. (10)
Для того чтобы получить необходимый допустимый базис для задачи линейного программирования, добавим формально остаточные искусственные переменные (
). Таким образом, уравнения (10) представляются в виде
(11)
Так как текущее управление 
– управление имеет любой знак, 
то сделаем необходимую замену
Тогда уравнения (11) примут вид
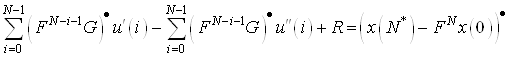(12)
Введем остаточные переменные в ограничения на управление
(13)
При объединении выражений (12) и (13) получаем 
ограничений.
Начальный допустимый базис состоит из остаточных и остаточных искусственных переменных
Формируем целевую функцию (по второму методу выбора начального допустимого базиса)
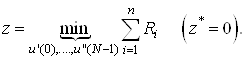(14)
б) Решение задачи быстродействия
Предположим, что 
, где – оптимальное число шагов. Так как значение нам неизвестно (но 
известно точно), выбираем некоторое начальное 
и решаем задачу линейного программирования (12)-(14).
При этом
Общее число столбцов в симплекс-таблице: 
Число базисных переменных: 
Сформируем 
строку. Имеем
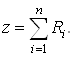
Выразим из уравнения (12) начальные базисные переменные 
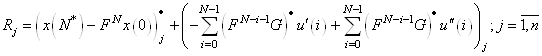
и подставим в целевую функцию. Получим 
– строку
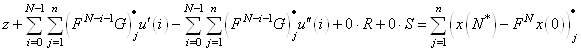(15)
Решаем задачу (12) – (14) симплекс-методом.
В случае,
если
, 
– малое число 
иначе
1) если 
увеличить
и целое,рвернуться к первому шагу формирования задачи линейного программирования;
2) если 
(не все управления будут равны предельным, могут быть, в том числе нулевые)), 
, уменьшить
, вернуться к первому шагу формирования задачи линейного программирования.
Решения данной задачи получено с помощью пакета Matlab 7.4 (скрипт SimplexMetod2.m): 
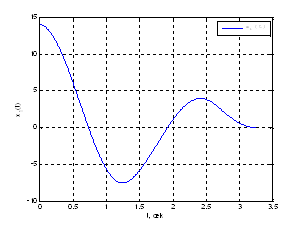
Рис. 14. График фазовой координаты 
.
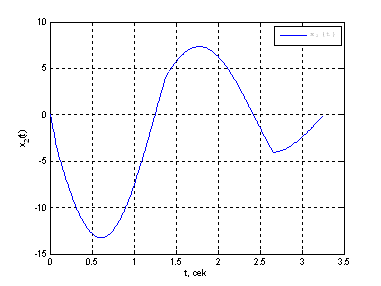
Рис. 15. График фазовой координаты 
.
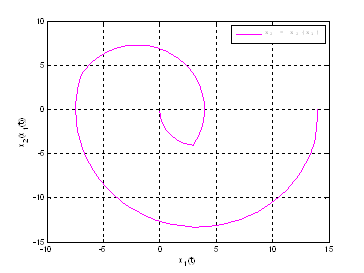
Рис. 16. График 
.
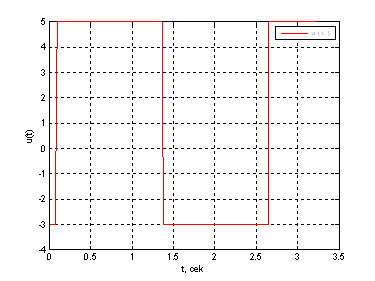
Рис. 17. График оптимального управления 
.
Выводы: Сравнивая полученные результаты с результатами полученными в ДЗ№2 по СУЛА, можно сделать вывод, что решения совпадают, с точностью до 
.
3. Оптимальная L – проблема моментов
3.1 Оптимальная L – проблема моментов в пространстве «вход-выход»
Укороченная система данного объекта имеет вид:
,
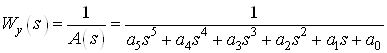где:
;
;
;
;
;
.
Полюса укороченной передаточной функции:
;
;
;
;
.
Заданы начальные и конечные условия:
, 
, 
.
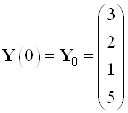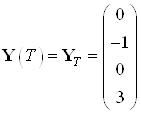Для определения начальных и конечных условий для 
воспользуемся следующей формулой:
,
Где матрица 
имеет следующий вид
,
где 
, 
.
ИПФ укороченной системы:
Составим фундаментальную систему решений:
ФСР: 
.
Составим матрицу 
.
, где 
– матрица Вронского
,
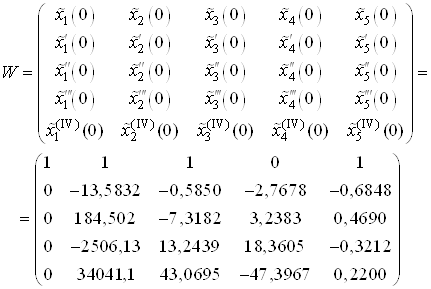
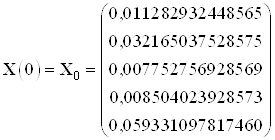Тогда
.
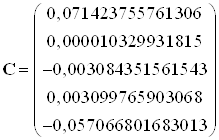Составим моментные уравнения (связь между входом и выходом):
Моментные функции определяются по следующей формуле
Составим моментные функции:
Найдем моменты по следующей формуле:
.
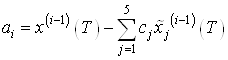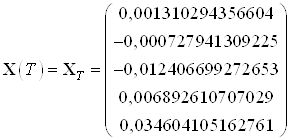
Числовое значение найденных моментов:
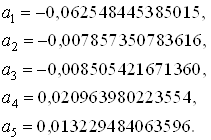
Составим функционал качества, который имеет следующий вид:
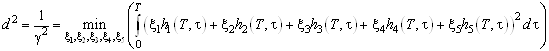
при условии, что :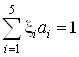
, т.е. 
Выразим из данного условия 
, тогда получим следующее равенство:
.
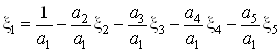Подставляя полученное равенство в функционал и заменяя 
их правыми частями получаем
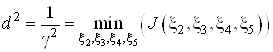
Найдем частные производные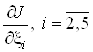 
и приравняем их к нулю. Решая полученную систему уравнений, определяем оптимальные значения коэффициентов 
, а вычислим по формуле
.
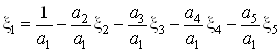Т.о. имеем:
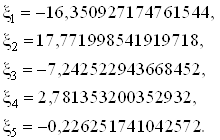
Минимальная энергия:
Найдем управление по следующей формуле:
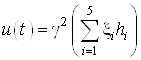
Тогда оптимальное управление
.
3.2 Оптимальная L – проблема моментов в пространстве состояний
Система задана в виде:
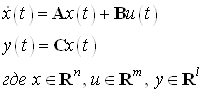
Решение ДУ имеет вид:
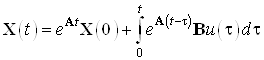, при 
имеем:
.
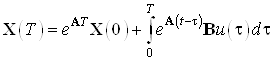Составим моментные уравнения:
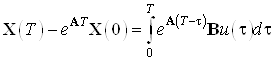
Подставляя необходимые данные в выше приведенные формулы, получим следующие моменты и моментные функции:
Числовое значение найденных моментов:
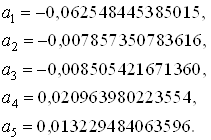
Моментные функции:
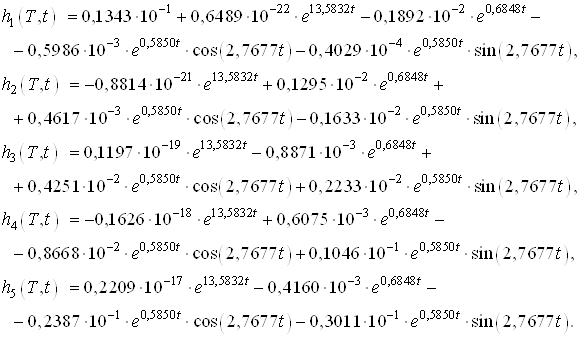
Заметим, что моменты и моментные функции совпадают с моментами и моментными функциями, найденными в пункте (а).
Из этого следует, что функционал, значения 
, управление и минимальная энергия будут иметь точно такие же числовые значения и аналитические выражения, как и в пункте (3.1).
Оптимальное управление имеет вид:
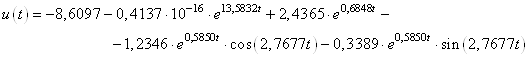
Проверим правильность полученного решения.
Эталонные значения координат в начальный и конечный момент времени:
,
,
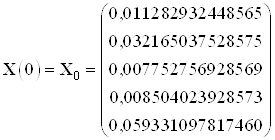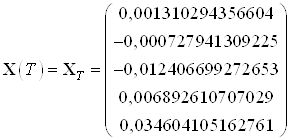
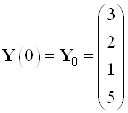Найденные значения координат в начальный и конечный момент времени:
, 
, 
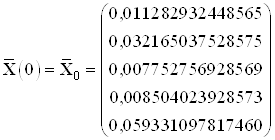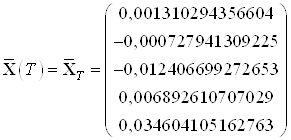
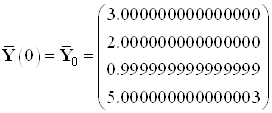Вычислим погрешность полученных результатов:
, 
, 
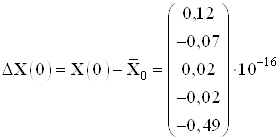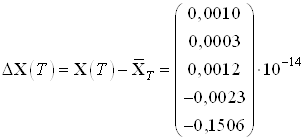
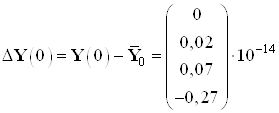Ниже представлены графики полученного решения с помощью скрипта Optimal_L_problem_moments.m.
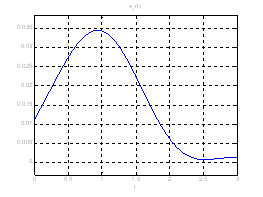
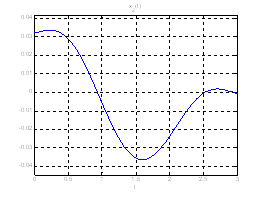
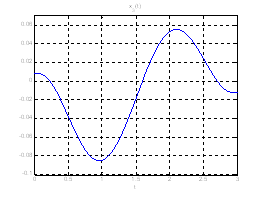
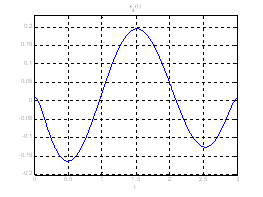
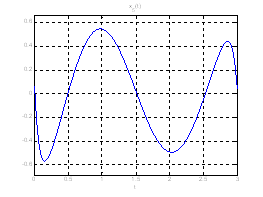
Рис. 18. Графики фазовых координат системы при переходе из 
в 
.
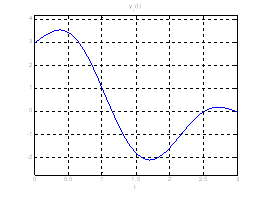
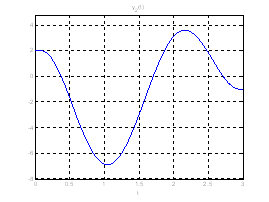
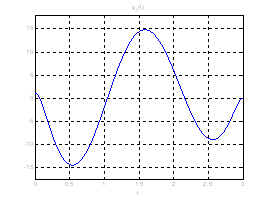
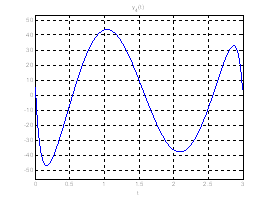
Рис. 19. Графики выходных координат системы при переходе из 
в 
.
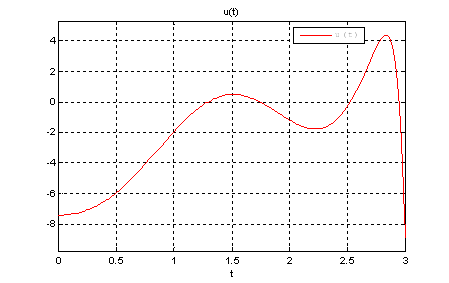
Рис.20. График оптимального управления .
Выводы:Задача перевода системы из начальной точки в конечную с помощью L-проблемы моментов в пространстве состояний и в пространстве вход-выход была решена с точностью до 12-го знака после запятой. Результаты, полученные при переводе системы из начальной точки в конечную, полностью совпадают.
4. Нахождение оптимального управления с использованием грамиана управляемости (критерий – минимизация энергии)
Система имеет вид:
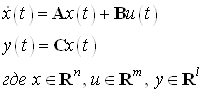
с начальными условиями:
,
.
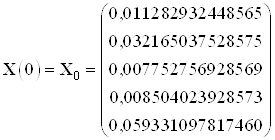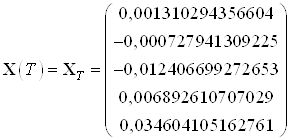
Составим матрицу управляемости и проверим управляемость системы:
.
Составим грамиан управляемости для данной системы:
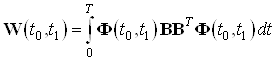
Найдем грамиан по формуле:
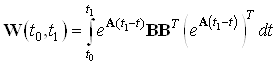
Тогда управление имеет вид:
.
или
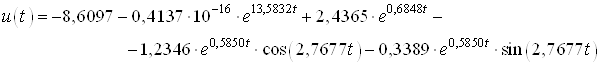
Ниже представлен график оптимального управления полученного с помощью скрипта Gramian_Uprav.m.:
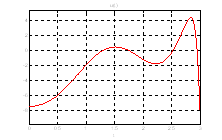
Рис.21. График оптимального управления .
Графики фазовых координат аналогичны, как и в оптимальной L – проблеме моментов.
Сравним управление, полученное в начальной и конечной точках в пунктах 3 и 4 соответственно:
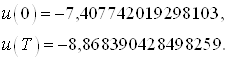и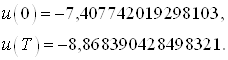 
Выводы:Как видно, значения граничных управлений совпадают. А это значит, что задача перевода объекта из начального состояния в конечное решена с высокой степенью точности и с минимальной энергией.
Графическое сравнение оптимальных управлений из пунктов 3 и 4:
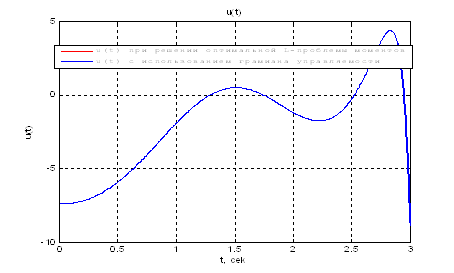
Рис.21. Сравнение графиков оптимального управления .
5. Аналитическое конструирование оптимальных регуляторов (АКОР)
5.1 Стабилизации объекта управления на полубесконечном интервале времени
Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме
Необходимо получить закон управления
минимизирующий функционал вида
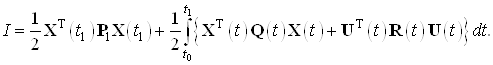
Начальные условия для заданной системы 
Моменты времени 
фиксированы. Матрицы 
— симметричные неотрицательно определенные:
матрица 
— положительно определенная:
Матричное дифференциальное уравнение Риккати имеет вид:
Если линейная стационарная система является полностью управляемой и наблюдаемой, то решение уравнения Риккати при 
стремится к установившемуся решению 
не зависящему от 
и определяется следующим алгебраическим уравнением:
В рассматриваемом случае весовые матрицы 
и в функционале не зависят от времени.
Оптимальное значение функционала равно
и является квадратичной функцией от начальных значений отклонения вектора состояния.
Таким образом, получаем, что при 
оптимальное управление приобретает форму стационарной обратной связи по состоянию
где 
— решение алгебраического матричного уравнения Риккати.
5.1.1. Решение алгебраического уравнения Риккати методом диагонализации
Для решения данной задачи найдем весовые матрицы и :
Выберем произвольно 
, тогда
Взяв значения 
из решения задачи L – проблемы моментов получим:
Матрицы системы имеют вид:
, 
.
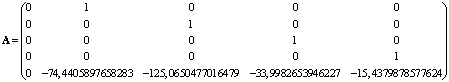
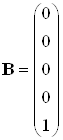Введем расширенный вектор состояния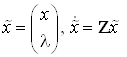 
.
Тогда матрица Zбудет иметь следующий вид: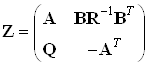 
,
или в численном виде
.
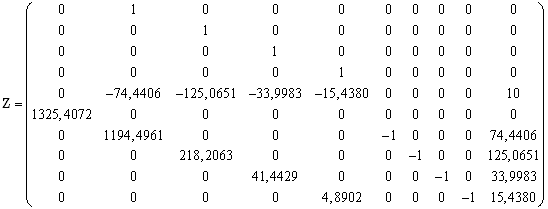Собственные значения матрицы 
: 
.
Зная собственные значения и собственные вектора матрицы Z, построим матрицу 
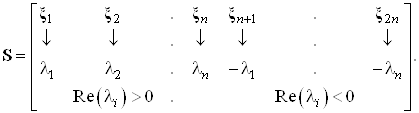
По определению все решения должны быть устойчивы при любых начальных условиях , т.е. при 
. Чтобы не оперировать комплексными числами, осуществим следующий переход. Пусть:
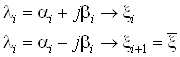
Тогда матрица формируется следующим образом:
.
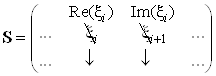Можно показать, что матрицу можно получить из прямой матрицы собственных векторов:
,
.
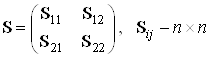Установившееся решение уравнения Риккати, полученное с помощью скрипта Solve_Riccati_Method_Diag.m. имеет вид:
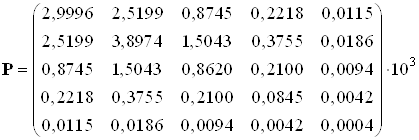
5.1.2 Решение алгебраического уравнения Риккати интегрированием в обратном времени до установившегося состояния
Весовые матрицы и такие же как и в пункте (5.1.1).
Матрицы 
тоже аналогичны.
Запишем уравнение Риккати
.
Зная, что 
, решаем уравнение методом обратного интегрирования на достаточно большом интервале (примерно 10 с.), получим установившееся решение с помощью скрипта
Solve_Riccati_Method_Revers_Integr.m.:
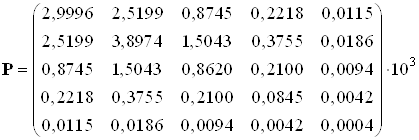
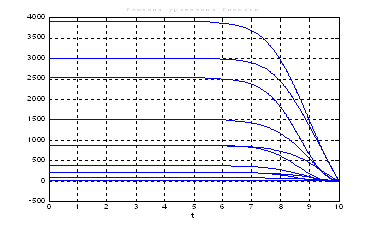
Рис.22. Графики решения уравнения Риккати.
Найдем разницу между решениями уравнения Риккати в пунктах 5.1.1 и 5.1.2:
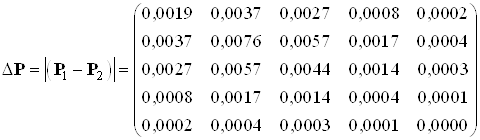
Выводы:сравнивая решения полученные в пунктах 5.1.1 и 5.1.2 можно сказать, что решения уравнения Риккати первым и вторым методами совпадают с заданной точностью. Погрешность расхождения решений невелика.
Используя скрипт AKOR_stabilizaciya_na_polybeskon_interval.m получим коэффициенты регулятора, фазовые координаты системы и управление.
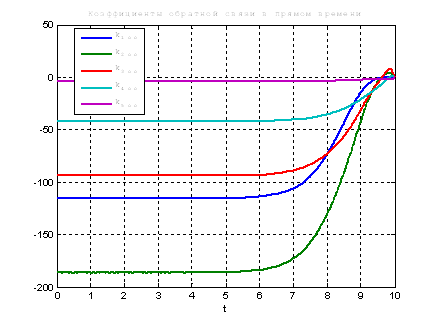
Рис.23. Графики коэффициентов регулятора обратной связи.
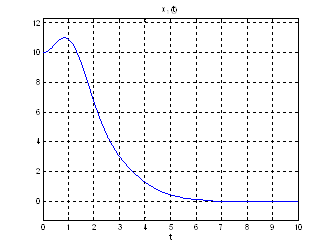
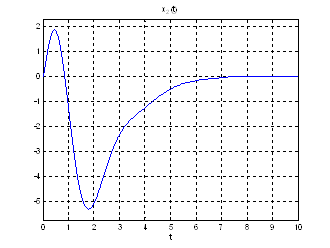
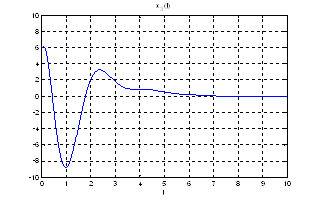
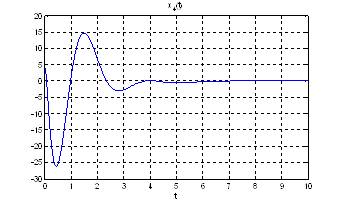
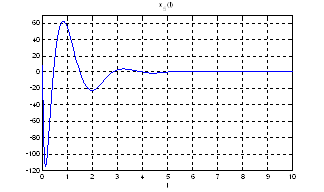
Рис.24. Графики фазовых координат.
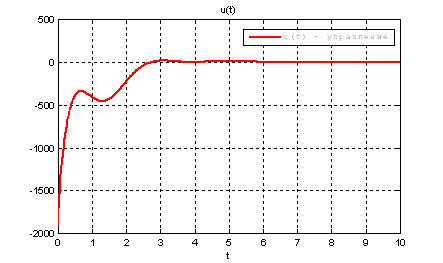
Рис.25. График управления.
Выводы:т.к. решения уравнения Риккати методом диагонализации и интегрирования в обратном времени дают практически одинаковый результат, то можно считать, что задача АКОР – стабилизации на полубесконечном интервале решена с заданной точностью.
5.2 Стабилизации объекта управления на конечном интервале времени
Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме
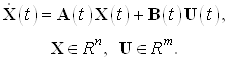
Начальные условия для заданной системы
Время стабилизации 
.
Необходимо получить закон управления
минимизирующий функционал вида
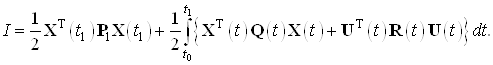
Закон оптимального управления в данной задаче имеет вид
Матричное дифференциальное уравнение Риккати будет иметь следующий вид:
Если обозначить 
то можно записать
Уравнение замкнутой скорректированной системы примет вид
Матрицы 
заданы в пункте 5.1.1.
Весовые матрицы и имеют следующий вид:
, 
.
Используя скрипт AKOR_stabilizaciya_na_konech_interval.m получили следующие результаты:
Рис.26. Графики решения уравнения Риккати.
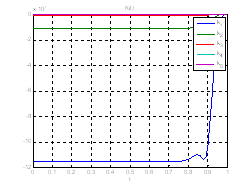
Рис.27. Графики коэффициентов регулятора обратной связи.
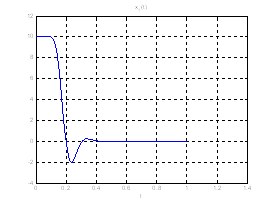
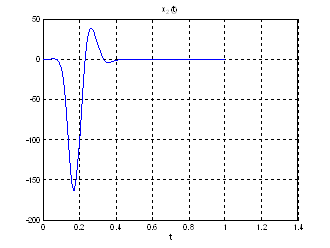
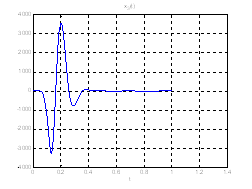
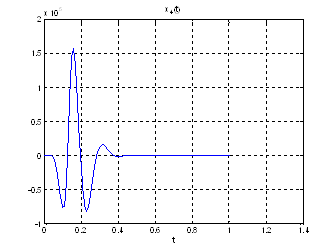
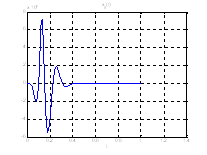
Рис.28. Графики фазовых координат.
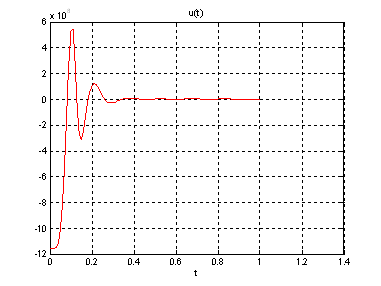
Рис.29. График управления.
Сравним, как стабилизируется система управления с постоянными и переменными коэффициентами регулятора обратной связи на начальном этапе:
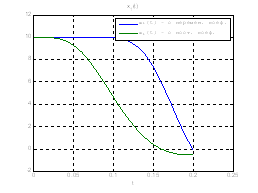
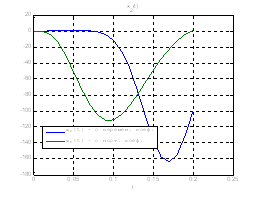
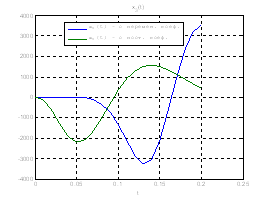
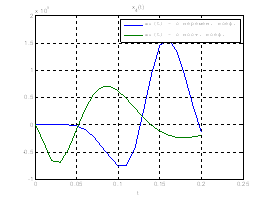
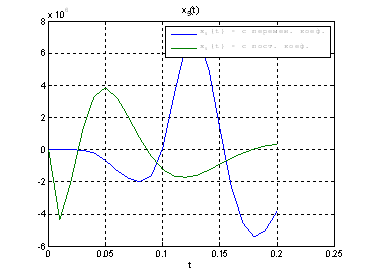
Рис.30. Графики фазовых координат.
Выводы:из графиков видно, что система, у которой коэффициенты регулятора меняются со временем, стабилизируется не хуже, чем, система, у которой коэффициенты регулятора не изменяются.
5.3 Задача АКОР – стабилизации для компенсации
известного возмущающего воздействия
Рассмотрим систему вида
,
где 
– возмущающее воздействие.
Матрицы заданы в пункте 5.1.1.
Весовые матрицы и имеют следующий вид:
, .
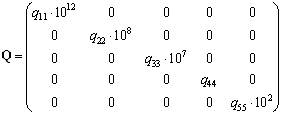Начальные условия для заданной системы 
.
Время стабилизации .
Задаем возмущающее воздействие только на первую координату, так как только она имеет значение
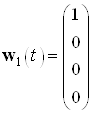и 
.
Решение задачи стабилизации сводится к решению уравнения Риккати
с начальными условиями: 
Введём вспомогательную вектор-функцию 
, ДУ которой имеет вид:
с начальными условиями: 
.
Управление определяется по формуле:
.
Используя скрипт AKOR_stabilizaciya_pri_vozmusheniyah.m, получили следующие результаты:
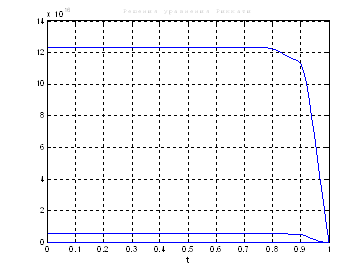
Рис.31. Графики решения уравнения Риккати.
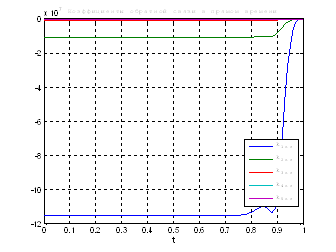
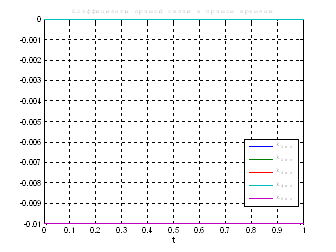
Рис.32. Графики коэффициентов регулятора обратной и прямой связи.
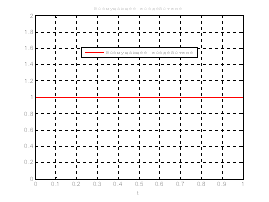
Рис.33. График возмущающего воздействия.
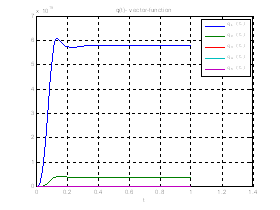
Рис.34. График вспомогательной вектор – функции.
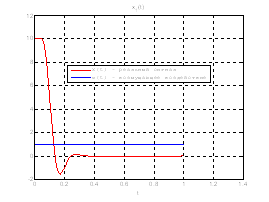
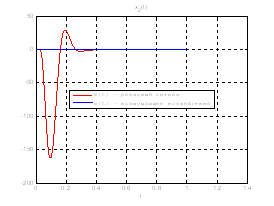
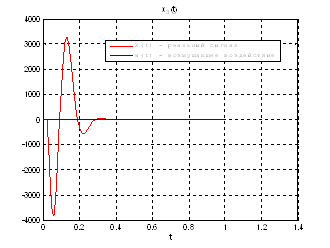
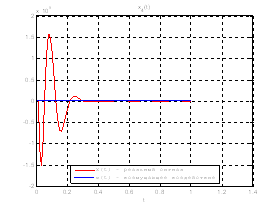
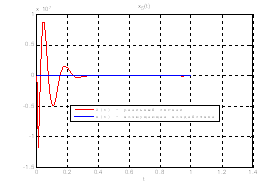
Рис.35. Графики фазовых координат.
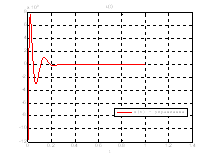
Рис.36. График управления.
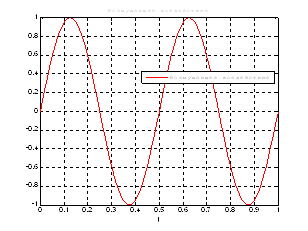
Рис.37. График возмущающего воздействия.
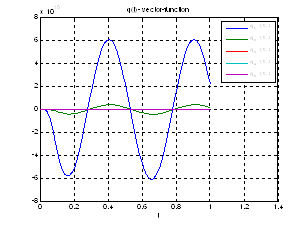
Рис.38. График вспомогательной вектор – функции.
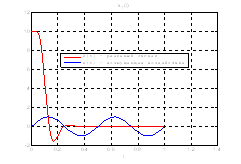
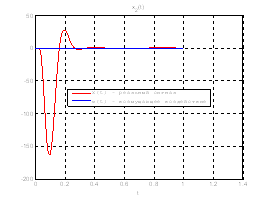
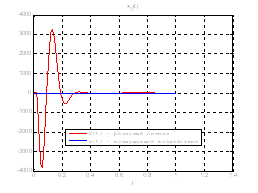
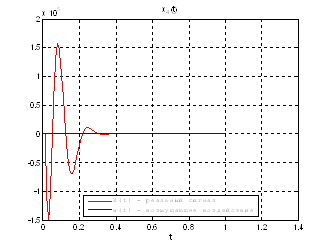
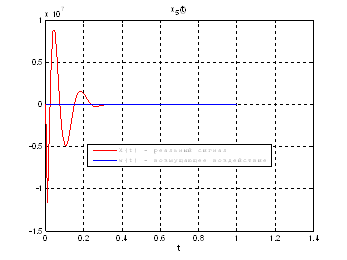
Рис.39. Графики фазовых координат.
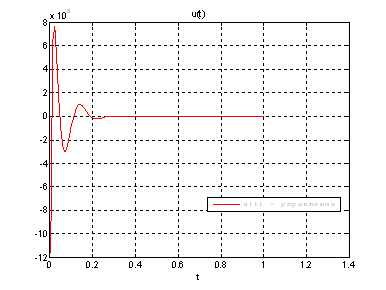
Рис.40. График управления.
Выводы: По графикам фазовых координат при различных воздействиях видно, что влияние возмущающего воздействия не существенно и фазовые координаты устанавливаются в ноль. При этом видно, что графики первой фазовой координаты при различных воздействиях мало отличаются друг от друга, т.е. система отрабатывает любое возмущение.
5.4 Задача АКОР для отслеживания известного задающего воздействия. I подход
Система задана в виде:
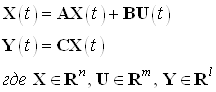
Матрицы заданы в пункте 5.1.1.
Весовые матрицы и имеют следующий вид:
, .
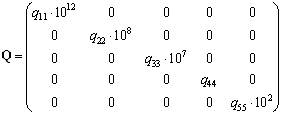Начальные условия для заданной системы .
Время слежения .
Задающее воздействие в виде системы ДУ
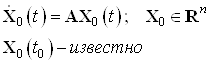
Начальные условия для воздействия:
.
Введем расширенный вектор состояния и расширенные матрицы 
,
,
.
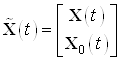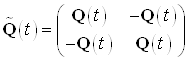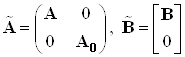Тогда новое описание системы имеет вид: